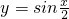Question

下列各函数中，最小正周期是π的函数是（　　）

• A．y=sin

  x

  2

• B．y=cos

  x

  2

• C．y=sin²x
• D．y=cos2

  x

  2

Answer 1

分析：找出选项A和B中的函数解析式中ω的值，代入周期公式T=

2π

|ω|

，可求出两选项中函数的最小正周期；把选项C和D中的函数利用二倍角的余弦函数公式化简后，找出函数解析式中ω的值，代入周期公式T=

2π

|ω|

，可求出两选项中函数的最小正周期，即可得到满足题意的选项．

解答：解：A、y=sin

x

2

，∵ω=

1

2

，∴T=4π，不合题意；
B、y=cos

x

2

，∵ω=

1

2

，∴T=4π，不合题意；
C、y=sin²x=

1

2

（1-cos2x）=-

1

2

cos2x+

1

2

，∵ω=2，∴T=π，符合题意；
D、y=cos²

x

2

=

1

2

（1+cosx）=

1

2

cosx-

1

2

，∵ω=1，∴T=2π，不合题意，
故选C

点评：此题考查了三角函数的周期性及其求法，涉及了二倍角的余弦函数公式，其中运用三角函数的恒等变形化简三角函数解析式，找出ω的值是解本题的关键．