题目内容
 (2011•济南二模)已知矩形ABCD与正三角形AED所在的平面互相垂直,M、N分别为棱BE、AD的中点,AB=1,AD=2,
(2011•济南二模)已知矩形ABCD与正三角形AED所在的平面互相垂直,M、N分别为棱BE、AD的中点,AB=1,AD=2,(1)证明:直线AM∥平面NEC;
(2)求二面角N-CE-D的大小.
分析:(1)方法一:取EC的中点F,连接FM,FN,利用中位线定理,结合直线平行的传递性,证明出四边形AMFN为平行四边形,从而得到AM∥NF,最后用直线与平面平行的判定定理,得到直线AM∥平面NEC;
方法二:设出平面NEC的一个法向量
,根据垂直向量的数量积为零,联解方程组得到法向量
的坐标,再通过计算
•
=0,得到法向量
与
垂直,从而得到直线AM∥平面NEC;
(2)方法一:先用面面垂直的性质证明出平面CDE⊥平面ADE,然后作NH⊥DE于H,则NH⊥面CDE,作HO⊥EC于O,连接
NO,然后用三垂线定理证出∠HON就是二面角N-CE-D的平面角,在正△ADE中求出NH长,在Rt△EDC中求出OH长,最后在Rt△NHO求出∠HON的正切,从而得到二面角N-CE-D的大小.
方法二:二面角N-CE-D的大小,即为平面NEC的法向量与平面DEC法向量的所成角大小.因此再设出平面DEC的一个法向量为
,根据垂直向量的数量积为零,联解方程组得到法向量
的坐标,利用向量的夹角公式计算出向量
、
的夹角余弦,从而得到向量
、
的夹角的大小,即为二面角N-CE-D的大小.
方法二:设出平面NEC的一个法向量
| n |
| n |
| n |
| AM |
| n |
| AM |
(2)方法一:先用面面垂直的性质证明出平面CDE⊥平面ADE,然后作NH⊥DE于H,则NH⊥面CDE,作HO⊥EC于O,连接
NO,然后用三垂线定理证出∠HON就是二面角N-CE-D的平面角,在正△ADE中求出NH长,在Rt△EDC中求出OH长,最后在Rt△NHO求出∠HON的正切,从而得到二面角N-CE-D的大小.
方法二:二面角N-CE-D的大小,即为平面NEC的法向量与平面DEC法向量的所成角大小.因此再设出平面DEC的一个法向量为
| m |
| m |
| m |
| n |
| m |
| n |
解答: 解:方法一:
解:方法一:
(1)取EC的中点F,连接FM,FN,
∵△EBC中,MF是中位线
∴FM∥BC,FM=
BC,…(2分)
∵AN∥BC,AN=
BC
∴FM∥BC且FM=BC,
∴四边形AMFN为平行四边形,
∴AM∥NF,…(4分)
∵AM?平面NEC,NF?平面NEC,
∴直线AM∥平面NEC; …(6分)
(2)由题设知平面ABCD⊥平面ADE,CD⊥AD,
∵平面ABCD∩平面ADE=AD,
∴CD⊥平面ADE
又∵CD?平面CDE,
∴平面CDE⊥平面ADE,
作NH⊥DE于H,则NH⊥平面CDE,作HO⊥EC于O,连接NO,
由三垂线定理可知NO⊥CE,
∴∠HON就是二面角N-CE-D的平面角,…(9分)
在正△ADE中,可得NH=
,在Rt△EDC中,可得OH=
,
故在Rt△NHO中,tan∠HON=
=
,…(11分)
所以二面角N-CE-D的大小为arctan
…(12分)
方法二:如图以N为坐标原点建立空间右手
直角坐标系,所以A(0,-1,0),B(0,-1,1)D(0,1,0),N(0,0,0),E(
,0,0),C(0,1,1),M(
,-
,
),…(1分)
(1)取EC的中点F,所以F(
,
,
),
设平面NEC的一个法向量为
=(x,y,1),因为
=(0,1,1),
=(
,0,0)
所以
•
=y+1=0,
•
=
x=0;所以
=(0,-1,1),…(3分)
因为
=(
,
,
),
•
=0,所以
⊥
…(5分)
因为AM?平面NEC,所以直线AM∥平面NEC…(7分)
(2)设平面DEC的一个法向量为
=(1,y,z),
因为
=(0,0,1),
=(
,-1,0)
所以
•
=z=0,x=
;
所以
=(1,
,0)…(9分)
cos<
,
>=
=
=-
…(11分)
因为二面角N-CE-D的大小为锐角,
所以二面角N-CE-D的大小为 arccos
…(12分)
 解:方法一:
解:方法一:(1)取EC的中点F,连接FM,FN,
∵△EBC中,MF是中位线
∴FM∥BC,FM=
| 1 |
| 2 |
∵AN∥BC,AN=
| 1 |
| 2 |
∴FM∥BC且FM=BC,
∴四边形AMFN为平行四边形,
∴AM∥NF,…(4分)
∵AM?平面NEC,NF?平面NEC,
∴直线AM∥平面NEC; …(6分)
(2)由题设知平面ABCD⊥平面ADE,CD⊥AD,
∵平面ABCD∩平面ADE=AD,
∴CD⊥平面ADE
又∵CD?平面CDE,
∴平面CDE⊥平面ADE,
作NH⊥DE于H,则NH⊥平面CDE,作HO⊥EC于O,连接NO,
由三垂线定理可知NO⊥CE,
∴∠HON就是二面角N-CE-D的平面角,…(9分)
在正△ADE中,可得NH=
| ||
| 2 |
3
| ||
| 10 |
故在Rt△NHO中,tan∠HON=
| NH |
| OH |
| ||
| 3 |
所以二面角N-CE-D的大小为arctan
| ||
| 3 |
方法二:如图以N为坐标原点建立空间右手
直角坐标系,所以A(0,-1,0),B(0,-1,1)D(0,1,0),N(0,0,0),E(
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(1)取EC的中点F,所以F(
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
设平面NEC的一个法向量为
| n |
| NC |
| NE |
| 3 |
所以
| n |
| NC |
| n |
| NE |
| 3 |
| n |
因为
| AM |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| n |
| AM |
| n |
| AM |
因为AM?平面NEC,所以直线AM∥平面NEC…(7分)
(2)设平面DEC的一个法向量为
| m |
因为
| DC |
| DE |
| 3 |
所以
| m |
| DC |
| n+1 |
| n |
所以
| m |
| 3 |
cos<
| n |
| m |
| ||||
|
|
-
| ||
|
| ||
| 4 |
因为二面角N-CE-D的大小为锐角,
所以二面角N-CE-D的大小为 arccos
| ||
| 4 |
点评:本题以一个特殊的四棱锥为载体,着重考查了空间直线与平面平行的判定和平面与平面所成角的求法等知识点,属于中档题.题中用利用空间向量证明线面平行和求平面间的夹角的方法,值得同学们关注.

练习册系列答案
相关题目
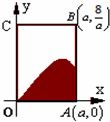 (2011•济南二模)如图,矩形OABC内的阴影部分是由曲线f(x)=sinx(x∈(0,π))及直线x=a(a∈(0,π))与x轴围成,向矩形OABC内随机投掷一点,若落在阴影部分的概率为
(2011•济南二模)如图,矩形OABC内的阴影部分是由曲线f(x)=sinx(x∈(0,π))及直线x=a(a∈(0,π))与x轴围成,向矩形OABC内随机投掷一点,若落在阴影部分的概率为