题目内容
(2011•济南二模)过点(0,1)且与曲线y=
在点(3,2)处的切线垂直的直线的方程为( )
| x+1 |
| x-1 |
分析:根据求导法则求出函数的导函数,然后把x=3代入导函数求出切线方程的斜率,然后根据两直线垂直时斜率的关系求出所求直线的斜率,由已知点的坐标和求出的斜率写出所求直线的方程即可.
解答:解:由y=
,得到y′=
=-
,
把x=3代入y′得:y′x=3=-
,
则所求直线方程的斜率为2,又所求直线过(0,1),
所求直线额方程为:y-1=2x,即2x-y+1=0.
故选A
| x+1 |
| x-1 |
| (x-1)-(x+1) |
| (x-1)2 |
| 2 |
| (x-1)2 |
把x=3代入y′得:y′x=3=-
| 1 |
| 2 |
则所求直线方程的斜率为2,又所求直线过(0,1),
所求直线额方程为:y-1=2x,即2x-y+1=0.
故选A
点评:此题考查学生会利用导数求曲线上过某点切线方程的斜率,掌握两直线垂直时斜率满足的关系,是一道基础题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
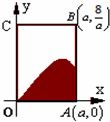 (2011•济南二模)如图,矩形OABC内的阴影部分是由曲线f(x)=sinx(x∈(0,π))及直线x=a(a∈(0,π))与x轴围成,向矩形OABC内随机投掷一点,若落在阴影部分的概率为
(2011•济南二模)如图,矩形OABC内的阴影部分是由曲线f(x)=sinx(x∈(0,π))及直线x=a(a∈(0,π))与x轴围成,向矩形OABC内随机投掷一点,若落在阴影部分的概率为