题目内容
若点M是△ABC的重心,则下列向量中与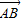 共线的是( )
共线的是( )A.
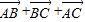
B.
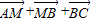
C.
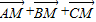
D.

【答案】分析:利用三角形重心的性质,到顶点距离等于到对边中点距离的二倍,利用向量共线的充要条件及向量的运算法则:平行四边形法则将 用三边对应的向量表示出.
用三边对应的向量表示出.
解答:解:∵点M是△ABC的重心,
设D,E,F分别是边BC,AC,AB的中点,
∴ =
= ,
,
同理 ,
,
 ,
,
∴
 =
= ,
,
∵零向量与任意的向量共线,
故选C.
点评:本题考查三角形的重心的性质:分每条中线为1:2;考查向量的运算法则:平行四边形法则.
 用三边对应的向量表示出.
用三边对应的向量表示出.解答:解:∵点M是△ABC的重心,
设D,E,F分别是边BC,AC,AB的中点,
∴
 =
= ,
,同理
 ,
, ,
,∴

 =
= ,
,∵零向量与任意的向量共线,
故选C.
点评:本题考查三角形的重心的性质:分每条中线为1:2;考查向量的运算法则:平行四边形法则.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若点M是△ABC的重心,则下列向量中与
共线的是( )
| AB |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、3
|