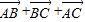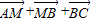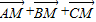题目内容
若点M是△ABC的重心，则下列向量中与| AB |
（1）
| AB |
| BC |
| AC |
（2）
| AM |
| MB |
| BC |
（3）
| AM |
| BM |
| CM |
（4）3
| AM |
| AC |
分析：对于（1），利用向量的运算法则将其化简得到
+
+
=2
不共线；对于（2）利用三角形的重心的性质：三等分中线得到
+
+
=
不与
共线，对于（3），利用三角形的重心的性质得到
+
+
=
与
；对于（4），利用三角形的重心性质得到3
+
=
+2
不与
共线．
| AB |
| BC |
| AC |
| AC |
| AM |
| MB |
| BC |
| AC |
| AB |
| AM |
| BM |
| CM |
| 0 |
| AB |
| AM |
| AC |
| AB |
| AC |
| AB |
解答：解：对于（1）
+
+
=2
不与
共线
对于（2）
+
+
=
+
=
不与
对于（3）
+
+
=
(
+
)+
(
+
)+
(
+
)=
与
对于（4）3
+
=
+
+AC不与
故答案为：（3）
| AB |
| BC |
| AC |
| AC |
| AB |
对于（2）
| AM |
| MB |
| BC |
| AB |
| BC |
| AC |
| AB |
对于（3）
| AM |
| BM |
| CM |
| 1 |
| 3 |
| AB |
| AC |
| 1 |
| 3 |
| BA |
| BC |
| 1 |
| 3 |
| CA |
| CB |
| 0 |
| AB |
对于（4）3
| AM |
| AC |
| AB |
| AC |
| AB |
故答案为：（3）
点评：解决三角形的重心问题一般利用三角形的重心的性质：重心到顶点的距离等于到对边中点的距离的二倍．
练习册系列答案
习题精选系列答案
相关题目
若点M是△ABC的重心，则下列向量中与
共线的是（ ）
| AB |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、3
|
+
+
等于( )
B.-6
C.0 D.6
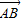共线的是（ ）
