题目内容
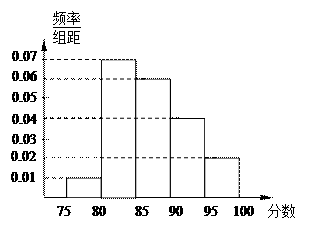
某学校随机抽取部分新生调查其上学路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学路上所需时间的范围是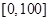 ,样本数据分组为
,样本数据分组为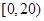 ,
,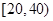 ,
,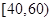 ,
,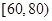 ,
,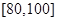 .
.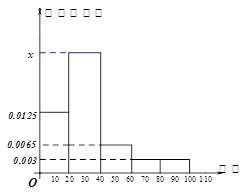
(1)求直方图中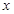 的值;
的值;
(2)如果上学路上所需时间不少于40分钟的学生可申请在学校住宿,请估计学校1000名新生中有多少名学生可以申请住宿.
(1) ;(2)250;
;(2)250;
解析试题分析:(1)根据频率分布直方图的小矩形的面积和为1,求得x值;
(2)利用频率分布直方图先求上学所需时间不少于40的学生的频率,再利用频率乘以总体个数可得1000名新生中有多少名学生可以申请住宿
1)由
则
(2)上学所需时间不少于40的学生的频率为:
估计学校1000名新生中有:
考点:用样本的频率分布估计总体分布;频率分布直方图.

练习册系列答案
相关题目
随着工业化以及城市车辆的增加,城市的空气污染越来越严重,空气质量指数API一直居高不下,对人体的呼吸系统造成了严重的影响.现调查了某市500名居民的工作场所和呼吸系统健康,得到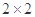 列联表如下:
列联表如下:
| | 室外工作 | 室内工作 | 合计 |
| 有呼吸系统疾病 | 150 | | |
| 无呼吸系统疾病 | | 100 | |
| 合计 | 200 | | |
(1)补全
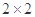 列联表;
列联表;(2)你是否有95%的把握认为感染呼吸系统疾病与工作场所有关;
某人摆一个摊位卖小商品,一周内出摊天数x与盈利y(百元),之间的一组数据关系见表:
 | 2 | 3 | 4 | 5 | 6 |
 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
已知
 ,
, ,
,(1)在下面坐标系中画出散点图;

(2)计算
 ,
, ,并求出线性回归方程;
,并求出线性回归方程;(3)在第(2)问条件下,估计该摊主每周7天要是天天出摊,盈利为多少?
某车间加工零件的数量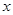 与加工时间
与加工时间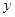 的统计数据如表:
的统计数据如表:
零件数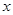 (个) (个) | 10 | 20 | 30 |
加工时间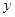 (分钟) (分钟) | 21 | 30 | 39 |
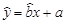 中的
中的 值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为( )
值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为( )A.112分钟 B.102分钟 C.94分钟 D.84分钟
甲乙两个班级均为40人,进行一门考试后,按学生考试成绩及格与不及格进行统计,甲班及格人数为36人,乙班及格人数为24人.
(1)根据以上数据建立一个 的列联表;(2)试判断成绩与班级是否有关?
的列联表;(2)试判断成绩与班级是否有关?
参考公式: ;
;
| P(K2>k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,解代表空气污染越严重:
| PM2.5日均浓度 | 0~35 | 35~75 | 75~115 | 115~150 | 150~250 | >250 |
| 空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
| 空气质量类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
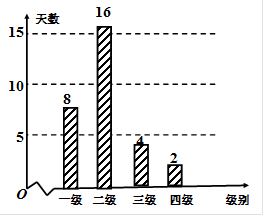
某市2013年3月8日—4月7日(30天)对空气质量指数PM2.5进行检测,获得数据后整理得到如下条形图:
(1)估计该城市一个月内空气质量类别为良的概率;
(2)从空气质量级别为三级和四级的数据中任取2个,求至少有一天空气质量类别为中度污染的概率.

 和样本方差
和样本方差 (同一组的数据用该组区间的中点值作代表);
(同一组的数据用该组区间的中点值作代表); 服从正态分布
服从正态分布 ,其中
,其中 近似为样本平均数
近似为样本平均数 近似为样本方差
近似为样本方差 ;
; 表示这100件产品中质量指标值位于区间
表示这100件产品中质量指标值位于区间 的产品件数.利用(i)的结果,求
的产品件数.利用(i)的结果,求 .
.
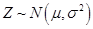 则
则 ,
, 。
。