题目内容
已知点 ,点
,点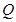 在曲线
在曲线 :
: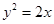 上.
上.
(1)若点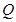 在第一象限内,且
在第一象限内,且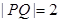 ,求点
,求点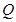 的坐标;
的坐标;
(2)求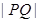 的最小值.
的最小值.
(1)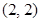 ;(2)
;(2)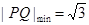 .
.
解析试题分析: (1) 本小题可以通过坐标法来处理,首先根据点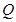 在第一象限内设其
在第一象限内设其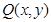 (
(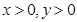 ),然后根据两点间距离公式
),然后根据两点间距离公式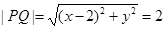 ,再结合点
,再结合点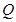 在曲线
在曲线 :
: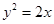 上,联立可解得
上,联立可解得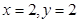 ,即点
,即点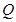 的坐标为
的坐标为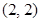 ;
;
(2) 本小题根据(1)中所得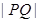
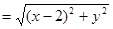 其中
其中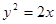 代入可得
代入可得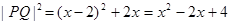
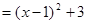 (
(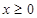 ),显然根据二次函数可知当
),显然根据二次函数可知当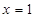 时,
时,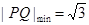 .
.
试题解析:设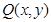 (
(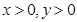 ),
),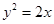
(1)由已知条件得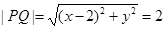 2分
2分
将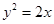 代入上式,并变形得,
代入上式,并变形得,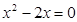 ,解得
,解得 (舍去)或
(舍去)或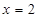 4分
4分
当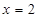 时,
时,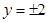
只有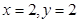 满足条件,所以点
满足条件,所以点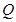 的坐标为
的坐标为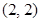 6分
6分
(2)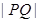
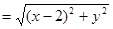 其中
其中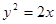 7分
7分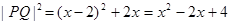
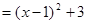 (
(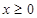 ) 10分
) 10分
当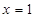 时,
时,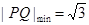 12分
12分
(不指出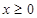 ,扣1分)
,扣1分)
考点:1.坐标法;2.二次函数求最值

练习册系列答案
相关题目
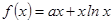 的图象在点
的图象在点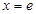 (e为自然对数的底数)处取得极值-1.
(e为自然对数的底数)处取得极值-1.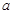 的值;
的值; 对任意
对任意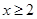 恒成立,求
恒成立,求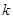 的取值范围.
的取值范围.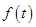 (单位:米)与生长年限t(单位:年)
(单位:米)与生长年限t(单位:年)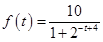 .(设该生物出生时t=0)
.(设该生物出生时t=0)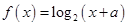 .
.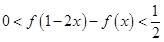 ,当
,当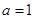 时,求
时,求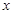 的取值范围;
的取值范围; 上奇函数
上奇函数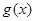 满足
满足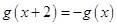 ,且当
,且当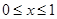 时,
时,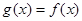 ,求
,求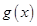 在
在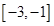 上的反函数
上的反函数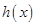 ;
;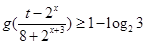 在
在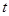 的取值范围.
的取值范围. ,h(x)=2alnx,
,h(x)=2alnx,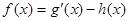 .
. 的单调性;
的单调性;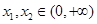 ,且
,且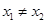 ,都有
,都有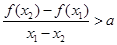

 的极值点,求实数a的值;
的极值点,求实数a的值; 在
在 上为增函数,求实数a的取值范围.
上为增函数,求实数a的取值范围.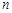 个工作台,将工艺流水线用如图
个工作台,将工艺流水线用如图 所示的数轴表示,各工作台的坐标分别为
所示的数轴表示,各工作台的坐标分别为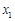 ,
,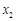 ,
, ,
,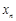 ,每个工作台上有若干名工人.现要在流水线上建一个零件供应站,使得各工作台上的所有工人到供应站的距离之和最短.
,每个工作台上有若干名工人.现要在流水线上建一个零件供应站,使得各工作台上的所有工人到供应站的距离之和最短.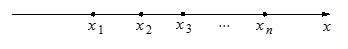
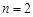 ,每个工作台上只有一名工人,试确定供应站的位置;
,每个工作台上只有一名工人,试确定供应站的位置;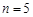 ,工作台从左到右的人数依次为
,工作台从左到右的人数依次为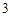 ,
,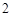 ,
,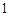 ,
, ,按每年
,按每年 衰减.
衰减. 年后,这种放射性元素的质量
年后,这种放射性元素的质量 与
与 的函数关系式;
的函数关系式; 时所经历的时间).(
时所经历的时间).( )
)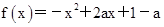 在
在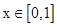 时有最大值2,求a的值.
时有最大值2,求a的值.