题目内容
已知数列{an}的前n项和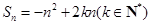 ,且
,且 的最大值为4.
的最大值为4.
(1)确定常数k的值,并求数列{an}的通项公式an;
(2)令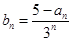 ,数列{bn}的前n项和为Tn,试比较Tn与
,数列{bn}的前n项和为Tn,试比较Tn与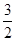 的大小.
的大小.
(1) ,
,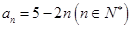 ;(2)详见解析.
;(2)详见解析.
解析试题分析:(1)先根据二次函数的相关知识以及 的最大值为
的最大值为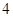 这些条件确定
这些条件确定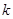 的值,再根据
的值,再根据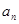 与
与 之间的关系
之间的关系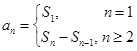 求出数列
求出数列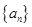 的通项公式;(2)先求出数列
的通项公式;(2)先求出数列 的通项公式,根据其通项结构选择错位相减法求出数列
的通项公式,根据其通项结构选择错位相减法求出数列 的前
的前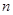 项和
项和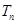 ,并根据
,并根据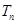 的表达式确定
的表达式确定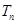 与
与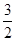 的大小.
的大小.
试题解析:(1)因为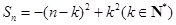 ,所以当
,所以当 时,
时, 取得最大值
取得最大值 .
.
依题意得 ,又
,又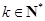 ,所以
,所以 .从而
.从而 .
.
当 时,
时, .
.
又 也适合上式,所以
也适合上式,所以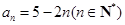 .
.
(2)由(1)得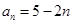 ,所以
,所以 .
.
所以 ①,
①, ②.
②.
由①-②得, ,
,
所以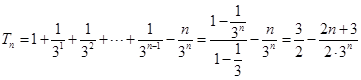 .
.
因为 ,所以
,所以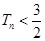 .
.
考点:数列通项、错位相减法

练习册系列答案
相关题目
 是公差不为零的等差数列,
是公差不为零的等差数列,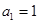 ,且
,且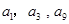 成等比数列.
成等比数列.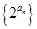 的前
的前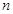 项和
项和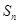 .
.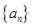 的前
的前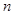 项和为
项和为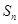 ,满足
,满足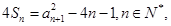 且
且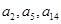 构成等比数列.
构成等比数列.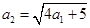 ;
;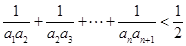 .
.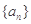 的前n项和为构成数列
的前n项和为构成数列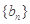 ,数列
,数列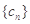 .
.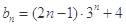 ,则
,则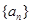 的奇数项是首项为1的等差数列,偶数项是首项为2的等比数列.数列
的奇数项是首项为1的等差数列,偶数项是首项为2的等比数列.数列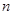 项和为
项和为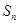 ,且满足
,且满足
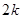 项和
项和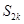 ;
;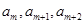 ,按原来的顺序成等差数列?若存在,求出所有满足条件的正整数
,按原来的顺序成等差数列?若存在,求出所有满足条件的正整数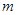 的值;若不存在,说明理由.
的值;若不存在,说明理由.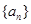 的前
的前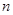 项和
项和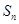 满足
满足 ,
,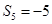 。
。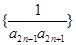 的前
的前 满足:
满足: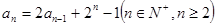 且
且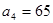 .(1)求数列
.(1)求数列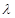 ,使数列
,使数列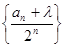 为等差数列?若存在,求出
为等差数列?若存在,求出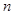 项和
项和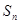 .
. 的图像上一点,数列
的图像上一点,数列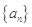 的前n项和
的前n项和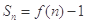 .
. 中,角
中,角 、
、 、
、 成等差数列,且
成等差数列,且 .
. 满足
满足 ,前
,前 项为和
项为和 ,若
,若 ,求
,求