题目内容
14.双曲线${x^2}-\frac{y^2}{2}=1$的渐近线方程为y=$±\sqrt{2}x$;离心率等于$\sqrt{3}$.分析 利用双曲线方程直接求解双曲线的渐近线方程以及离心率即可.
解答 解:双曲线${x^2}-\frac{y^2}{2}=1$的渐近线方程为:的渐近线方程为y=±2x;
a=1,b=$\sqrt{2}$,c=$\sqrt{3}$,所以双曲线的离心率为:$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题考查双曲线的简单性质的应用,考查计算能力.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
5.函数f(x)=e-x的导数是( )
| A. | -e-x | B. | e-x | C. | -ex | D. | ex |
9.已知数列{an}的前n项和为Sn,且2,Sn,an成等差数列,则S17=( )
| A. | 0 | B. | 2 | C. | -2 | D. | 34 |
3.设复数Z1,Z2在复平面内的对应点关于虚轴对称,Z1(1-i)=3-i,则Z2=( )
| A. | 2+i | B. | 2-i | C. | -2+i | D. | -2-i |
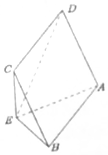 如图,在几何体ABCDE中,ABCD为正方形,CE⊥平面ABE,且异面直线AD、CE所成的角为30°.
如图,在几何体ABCDE中,ABCD为正方形,CE⊥平面ABE,且异面直线AD、CE所成的角为30°.