题目内容
一元二次方程mx2+(2m-3)x+(m-2)=0的两个实数根为tanα和tanβ,求tan(α+β)的取值范围及其最小值.
解:由方程有实根,得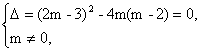
所以m的取值范围为m≤![]() 且m≠0;
且m≠0;
由韦达定理tanα+tanβ=![]() ,tanαtanβ=
,tanαtanβ=![]() ,
,
代入和角公式,得tan(α+β)=![]() ≥
≥![]() ,
,
所以tan(α+β)的取值范围为[-![]() ,
,![]() )∪(
)∪(![]() ,+∞),最小值为-
,+∞),最小值为-![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
一元二次方程mx2+(2m-3)x+(m-2)=0的两个实数根为tanα和tanβ,求tan(α+β)的取值范围及其最小值.
解:由方程有实根,得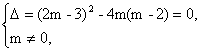
所以m的取值范围为m≤![]() 且m≠0;
且m≠0;
由韦达定理tanα+tanβ=![]() ,tanαtanβ=
,tanαtanβ=![]() ,
,
代入和角公式,得tan(α+β)=![]() ≥
≥![]() ,
,
所以tan(α+β)的取值范围为[-![]() ,
,![]() )∪(
)∪(![]() ,+∞),最小值为-
,+∞),最小值为-![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案