题目内容
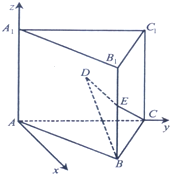
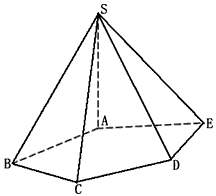
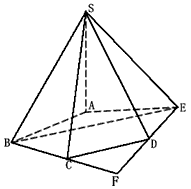
如图,在五棱锥S-ABCDE中,SA⊥底面ABCDE,SA=AB=AE=2,BC=DE=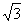 ,∠BAE=∠BCD=∠CDE=120°,
,∠BAE=∠BCD=∠CDE=120°,
(Ⅰ)求异面直线CD与SB所成的角(用反三角函数值表示);
(Ⅱ)证明BC⊥平面SAB;
(Ⅲ)用反三角函数值表示二面角B-SC-D的大小。
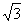 ,∠BAE=∠BCD=∠CDE=120°,
,∠BAE=∠BCD=∠CDE=120°,(Ⅰ)求异面直线CD与SB所成的角(用反三角函数值表示);
(Ⅱ)证明BC⊥平面SAB;
(Ⅲ)用反三角函数值表示二面角B-SC-D的大小。
| 解:(Ⅰ)连结BE,延长BC、ED交于点F, 则∠DCF=∠CDF=60°, ∴△CDF为正三角形, ∴CF=DF, 又BC=DE, ∴BF=EF, 因此,△BFE为正三角形, ∴∠FBE=∠FCD=60°, ∴BE∥CD, 所以∠SBE(或其补角)就是异面直线CD与SB所成的角, ∵SA⊥底面ABCDE,且SA=AB=AE=2, ∴SB=  , ,又∠BAE=120°, 所以BE= 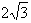 , ,从而 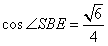 , ,∴∠SBE= 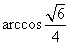 , ,所以异面直线CD与SB所成的角为  。 。(Ⅱ)由题意,△ABE是等腰三角形,∠BAE=120°, 所以∠ABE=30°, 又∠FBE=60°, ∴∠ABC=90°, 所以BC⊥BA, ∵SA⊥底面ABCDE,BC 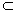 底面ABCDE, 底面ABCDE, ∴SA⊥BC, 又SA∩BA=A, ∴BC⊥平面SAB。 (Ⅲ)二面角B-SC-D的大小为 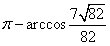 。 。 |
 |

练习册系列答案
相关题目