题目内容
9. 底面为菱形的直棱柱ABCD-A1B1C1D1中,E、F分别为棱A1B1、A1D1的中点.
底面为菱形的直棱柱ABCD-A1B1C1D1中,E、F分别为棱A1B1、A1D1的中点.(Ⅰ)在图中作一个平面α,使得BD?α,且平面AEF∥α,(不必给出证明过程,只要求作出α与直棱柱ABCD-A1B1C1D1的截面.)
(II)若AB=AA1=2,∠BAD=60°,求平面AEF与平面α的距离d.
分析 (Ⅰ)取B1C1的中点H,C1D1的中点G,平面BHGD就是所求平面α.
(Ⅱ)取BC中点M,以D为原点,DA为x轴,DM为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出平面AEF与平面α的距离.
解答 解:(Ⅰ)取B1C1的中点H,C1D1的中点G,连结BH、GH、DH,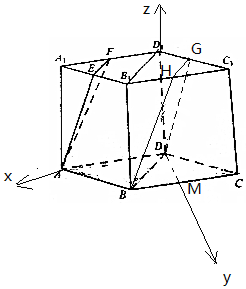
则平面BHGD就是所求平面α,
α与直棱柱ABCD-A1B1C1D1的截面为平面BHGD.
(Ⅱ)∵菱形的直棱柱ABCD-A1B1C1D1中,AB=AA1=2,∠BAD=60°,
∴取BC中点M,以D为原点,DA为x轴,DM为y轴,DD1为z轴,建立空间直角坐标系,
A(2,0,0),D(0,0,0),B(1,$\sqrt{3}$,0),H(0,$\sqrt{3}$,2),
$\overrightarrow{DA}$=(2,0,0),$\overrightarrow{DB}$=(1,$\sqrt{3}$,0),$\overrightarrow{DH}$=(0,$\sqrt{3}$,2),
设平面α(即平面BHGD)的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{DB}=x+\sqrt{3}y=0}\\{\overrightarrow{n}•\overrightarrow{DH}=\sqrt{3}y+2z=0}\end{array}\right.$,取y=2,得$\overrightarrow{n}$=(-2$\sqrt{3}$,2,-$\sqrt{3}$),
∴平面AEF与平面α的距离d=$\frac{|\overrightarrow{DA}•\overrightarrow{n}|}{|\overrightarrow{n}|}$=$\frac{4\sqrt{3}}{\sqrt{12+4+3}}$=$\frac{4\sqrt{57}}{19}$.
点评 本题考查满足面面平行的平面的作法,考查两平面间的距离的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

| A. | |$\overrightarrow{a}$|=|$\overrightarrow{b}$| | B. | $\overrightarrow{a}$•$\overrightarrow{b}$=$\frac{1}{2}$ | C. | $\overrightarrow{a}$⊥$\overrightarrow{b}$ | D. | ($\overrightarrow{a}$-$\overrightarrow{b}$)⊥$\overrightarrow{b}$ |
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $2\sqrt{2}$ | D. | 3 |
| A. | c>b>a | B. | b>a>c | C. | c>a>b | D. | a>b>c |
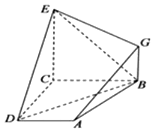 如图,已知四边形ABCD和BCGE均为直角梯形,AD∥BC,CE∥BG且∠BCD=∠BCE=$\frac{π}{2}$,平面ABCD⊥平面BCGE,BC=CD=CE=2AD=2BG=2.
如图,已知四边形ABCD和BCGE均为直角梯形,AD∥BC,CE∥BG且∠BCD=∠BCE=$\frac{π}{2}$,平面ABCD⊥平面BCGE,BC=CD=CE=2AD=2BG=2.