题目内容
(1)化简:0.25-1×(
)
×(
)
;
(2)已知2lg(x-2y)=lgx+lgy,求log
的值.
| ||
| 2 |
| 1 |
| 2 |
| 27 |
| 4 |
| 1 |
| 4 |
(2)已知2lg(x-2y)=lgx+lgy,求log
| 2 |
| y |
| x |
分析:(1)正确应用指数幂的运算法则,直接逐项求值后,再计算出最后结果.
(2)先利用对数的运算法则得出(x-2y)2=xy,移向整理得出x=4y,代入原式求值即可.注意x.y 的取值使对数式有意义.
(2)先利用对数的运算法则得出(x-2y)2=xy,移向整理得出x=4y,代入原式求值即可.注意x.y 的取值使对数式有意义.
解答:解:(1)原式=4×2-
×3
×27
×4-
=4×2-1×3
=6.
(2)根据题意,
得
解得
因此x=4y.
所以log
=log
4=4.
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
=4×2-1×3
=6.
(2)根据题意,
得
|
解得
|
因此x=4y.
所以log
| 2 |
| y |
| x |
| 2 |
点评:本题考查指数幂的运算法则,对数的运算法则,准确应用公式是关键,对数运算要注意字母的取值范围.

练习册系列答案
相关题目
(1)化简与求值:(0.0081)-
-[3(
)0]-1•[81-0.25+(
)-
]-
-10×0.027
;
(2)化简与求值:log2
+log212-
log242-1.
| 1 |
| 4 |
| 7 |
| 8 |
| 27 |
| 8 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
(2)化简与求值:log2
|
| 1 |
| 2 |
 ×
× ;
;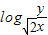 的值.
的值.