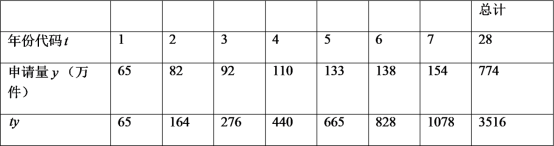题目内容
【题目】若定义在R上的函数![]() 满足:对于任意实数x、y,总有
满足:对于任意实数x、y,总有![]() 恒成立,我们称
恒成立,我们称![]() 为“类余弦型”函数.
为“类余弦型”函数.
![]() 已知
已知![]() 为“类余弦型”函数,且
为“类余弦型”函数,且![]() ,求
,求![]() 和
和![]() 的值;
的值;
![]() 在
在![]() 的条件下,定义数列
的条件下,定义数列![]() 2,3,
2,3,![]() 求
求![]() 的值.
的值.
![]() 若
若![]() 为“类余弦型”函数,且对于任意非零实数t,总有
为“类余弦型”函数,且对于任意非零实数t,总有![]() ,证明:函数
,证明:函数![]() 为偶函数,设有理数
为偶函数,设有理数![]() ,
,![]() 满足
满足![]() ,判断
,判断![]() 和
和![]() 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
【答案】(1)![]() ,
,![]() (2)
(2)![]() (3)证明见解析,
(3)证明见解析,![]() ,证明见解析
,证明见解析
【解析】
![]() 是抽象函数基础题,令
是抽象函数基础题,令![]() ,求得
,求得![]() ;令
;令![]() ,求得
,求得![]() ;
;
![]() 对于此数列,需要求其通项,而求通项又需要递推公式,令
对于此数列,需要求其通项,而求通项又需要递推公式,令![]() ,
,![]() ,利用题中关系式推导出递推公式
,利用题中关系式推导出递推公式![]() ,求通项然后利用对数的运算法则求解答案;
,求通项然后利用对数的运算法则求解答案;
![]() 属于难题,因为
属于难题,因为![]() 的铺垫,代入特定的数即令
的铺垫,代入特定的数即令![]() ,y为任意实数即可证明偶函数,证明
,y为任意实数即可证明偶函数,证明![]() 与
与![]() 的大小关系需要定义新的数列,又因为题目中的有理数条件,要充分利用分数的特点.
的大小关系需要定义新的数列,又因为题目中的有理数条件,要充分利用分数的特点.
解:![]() 令
令![]() ,
,![]() ,则
,则![]() ,所以
,所以![]() .
.
令![]() ,
,![]() ,则
,则![]() ,所以
,所以![]() .
.
![]() 令
令![]() ,
,![]() ,其中n是大于1的整数,则
,其中n是大于1的整数,则![]() ,所以
,所以![]() ,即
,即![]() .
.
又因为![]() ,所以数列
,所以数列![]() 是首项为3,公比为2的等比数列,所以
是首项为3,公比为2的等比数列,所以![]() ,则
,则![]() .
.
所以原式![]() .
.
(3)证明:由题意函数![]() 定义域为R关于原点对称,
定义域为R关于原点对称,
令![]() ,y为任意实数,则
,y为任意实数,则![]() ,即
,即![]() ,所以
,所以![]() 是偶函数.
是偶函数.
令N为![]() ,
,![]() 分母的最小公倍数,并且
分母的最小公倍数,并且![]() ,
,![]() ,
,![]() 都是自然数,并且
都是自然数,并且![]() .
.
令数列![]() 满足
满足![]() ,
,![]() ,1,
,1,![]() 下证:数列
下证:数列![]() 单调递增.
单调递增.
![]() ,所以
,所以![]() ;
;
![]() 若
若![]() ,n是正整数,即
,n是正整数,即![]() ;
;
令![]() ,
,![]() ,则
,则![]() ,即
,即![]() .
.
所以![]() .
.
综上,数列![]() 单调递增,所以
单调递增,所以![]() ,又因为
,又因为![]() 是偶函数,所以
是偶函数,所以![]()

练习册系列答案
相关题目