题目内容
【题目】已知椭圆
（
）的离心率为
，且经过点
.
（1）求椭圆
的方程；
（2）过点
作直线
与椭圆交于不同的两点
，
，试问在
轴上是否存在定点
使得直线
与直线
恰关于轴对称？若存在，求出点的坐标；若不存在，说明理由.
【答案】(1) 
(2)见解析
【解析】
（1）由题得a,b,c的方程组求解即可（2）直线
与直线
恰关于
轴对称，等价于
的斜率互为相反数，即
，整理
.设直线
的方程为
，与椭圆
联立，将韦达定理代入整理即可.
(1)由题意可得
，
，又
，
解得
，
.
所以，椭圆的方程为
(2)存在定点
，满足直线与直线恰关于轴对称.
设直线的方程为，与椭圆联立，整理得，
.
设
，
，定点
.(依题意
则由韦达定理可得，
，
.
直线与直线恰关于轴对称，等价于的斜率互为相反数.
所以，，即得
.
又
，
，
所以，
，整理得，.
从而可得，
，
即
，
所以，当
，即时，直线与直线恰关于轴对称成立. 特别地，当直线为轴时，也符合题意. 综上所述，存在轴上的定点，满足直线与直线恰关于轴对称.
【题目】若无穷数列
满足：
，当
，
时．
其中
表示
，
，
，
中的最大项
，有以下结论：
若数列是常数列，则
若数列是公差
的等差数列，则
；
若数列是公比为q的等比数列，则
则其中正确的结论是______
写出所有正确结论的序号
【题目】2014年7月18日15时，超强台风“威马逊”登陆海南省．据统计，本次台风造成全省直接经济损失119.52亿元．适逢暑假，小明调查住在自己小区的50户居民由于台风造成的经济损失，作出如下频率分布直方图：
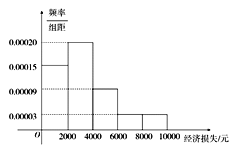
经济损失 4000元以下 | 经济损失 4000元以上 | 合计 | |
捐款超过500元 | 30 | ||
捐款低于500元 | 6 | ||
合计 |
(1)台风后区委会号召小区居民为台风重灾区捐款，小明调查的50户居民捐款情况如上表，在表格空白处填写正确数字，并说明是否有
以上的把握认为捐款数额是否多于或少于500元和自身经济损失是否到4000元有关？
(2)台风造成了小区多户居民门窗损坏，若小区所有居民的门窗均由李师傅和张师傅两人进行维修，李师傅每天早上在7：00到8：00之间的任意时刻来到小区，张师傅每天早上在7：30到8：30分之间的任意时刻来到小区，求连续3天内，李师傅比张师傅早到小区的天数的数学期望.
附：临界值表
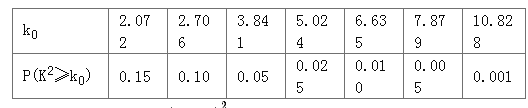
参考公式： 
.
