题目内容
设z是虚数,ω=z+![]() 是实数,且-1<ω<2.
是实数,且-1<ω<2.
(1)求|z|的值及z的实部的取值范围;
(2)设u=![]() ,求证:u是纯虚数;
,求证:u是纯虚数;
(3)求ω-u2的最小值.
(1)解:∵ω∈R,∴z+![]() =
=![]() .
.
∴z+![]() =
=![]() +
+![]() .∴z-
.∴z-![]() +
+![]() -
-![]() =0.
=0.
∴(z-![]() )(1-
)(1-![]() )=0.∴z=
)=0.∴z=![]() 或z·
或z·![]() =1.
=1.
∵z是虚数,∴z·z=1,|z|=1.
设z=x+yi,则y≠0.
ω=z+![]() =z+
=z+![]() =z+
=z+![]() =2x.
=2x.
∴-1<2x<2.∴-![]() <x<1.
<x<1.
(2)证明:u=![]()
=![]()
=![]() .故是纯虚数.
.故是纯虚数.
(3)解:ω-u2=z+![]() -(
-(![]() )2=(x+yi)+(x-yi)-(
)2=(x+yi)+(x-yi)-(![]() )2
)2
=2x+[![]() ]2
]2
=2x+![]() =2x+
=2x+![]()
=2[(x+1)+![]() ]-3.
]-3.
∵x∈(-![]() ,1),∴x+1>0.
,1),∴x+1>0.
∴ω-u2≥2×2-3=1.
当x+1=![]() ,即x=0时,上式取等号.
,即x=0时,上式取等号.
∴ω-u2的最小值是1.

练习册系列答案
相关题目
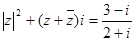 (i为虚数单位)
(i为虚数单位) 是实数,且-1<ω<2
是实数,且-1<ω<2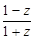 ,求证:u为纯虚数;(5分)
,求证:u为纯虚数;(5分)