题目内容
设z是虚数,ω=z+(1)求|z|的值及z的实部的取值范围;
(2)设u=![]() ,求证:u为纯虚数;
,求证:u为纯虚数;
(3)求ω-u2的最小值.
思路解析:条件与复数的概念有关系,不妨设z=a+bi(a、b∈R)且b≠0,从而转化为实数问题.
(1)解:设z=a+bi(a、b∈R)且b≠0,则ω=a+bi+![]() +(b-
+(b-![]() )i.
)i.
∵ω是实数,b≠0,∴a2+b2=1,即|z|=1.于是ω=2a,-1<ω=2a<2.
∴![]() <a<1.故z的取值范围是(
<a<1.故z的取值范围是(![]() ,1).
,1).
(2)证明:u=![]()
∵a∈(![]() ,1),且b≠0,∴u为纯虚数.
,1),且b≠0,∴u为纯虚数.
(3)解:ω-u2=2a-(![]() )2=2a+
)2=2a+![]()
=![]() .
.
∵![]() <a<1,∴a+1>0.
<a<1,∴a+1>0.
于是ω-u2=2(a+1)+![]() -3≥2×2-3=1.
-3≥2×2-3=1.
当且仅当a+1=![]() ,即a=0时等号成立.ω-u2的最小值为1,此时z=±i.
,即a=0时等号成立.ω-u2的最小值为1,此时z=±i.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
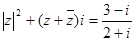 (i为虚数单位)
(i为虚数单位) 是实数,且-1<ω<2
是实数,且-1<ω<2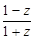 ,求证:u为纯虚数;(5分)
,求证:u为纯虚数;(5分)