题目内容
设z是虚数,ω=z+| 1 |
| z |
(1)求|z|的值及z的实部的取值范围;
(2)设u=
| 1-z |
| 1+z |
分析:(1)设出复数z,写出ω的表示式,进行复数的运算,把ω整理成最简形式,根据所给的ω的范围,得到ω的虚部为0,实部属于这个范围,得到z的实部的范围.
(2)根据设出的z,整理u的代数形式,进行复数的除法的运算,整理成最简形式,根据上一问做出的复数的模长是1,得到u是一个纯虚数.
(2)根据设出的z,整理u的代数形式,进行复数的除法的运算,整理成最简形式,根据上一问做出的复数的模长是1,得到u是一个纯虚数.
解答:解:设z=x+yi(x,y∈R,y≠0)
(1)ω=z+
=(x+
)+(y-
)i
∵-1<ω<2,∴y-
=0,
又∵y≠0,∴x2+y2=1即|z|=1
∵-1<x+
<2?-1<2x<2,
∴-
<x<1
即z的实部的取值范围是(-
,1)
(2)u=
=
=
∵x2+y2=1,∴u=
i
又∵y≠0,
∴u是纯虚数.
(1)ω=z+
| 1 |
| z |
| x |
| x2+y2 |
| y |
| x2+y2 |
∵-1<ω<2,∴y-
| y |
| x2+y2 |
又∵y≠0,∴x2+y2=1即|z|=1
∵-1<x+
| x |
| x2+y2 |
∴-
| 1 |
| 2 |
即z的实部的取值范围是(-
| 1 |
| 2 |
(2)u=
| 1-z |
| 1+z |
| (1-x-yi)(1+x-yi) |
| (1+x)2+y2 |
| (1-x2-y2)-2yi |
| (1+x)2+y2 |
∵x2+y2=1,∴u=
| -2y |
| (1+x)2+y2 |
又∵y≠0,
∴u是纯虚数.
点评:本题考查复数的代数形式的运算,本题是一个运算量比较大的问题,题目的运算比较麻烦,解题时注意数字不要出错.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
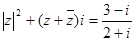 (i为虚数单位)
(i为虚数单位) 是实数,且-1<ω<2
是实数,且-1<ω<2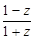 ,求证:u为纯虚数;(5分)
,求证:u为纯虚数;(5分)