题目内容
14.{an}为等差数列,Sn为其前n项和,a7=5,S7=21,则S10=40.分析 利用等差数列的通项公式及其前n项和公式即可得出.
解答 解:设等差数列{an}的公差为d,
∵a7=5,S7=21,
∴$\left\{\begin{array}{l}{{a}_{1}+6d=5}\\{7{a}_{1}+\frac{7×6}{2}×d=21}\end{array}\right.$,
解得a1=1,d=$\frac{2}{3}$.
则S10=10×1+$\frac{10×9}{2}×\frac{2}{3}$=40.
故答案为:40.
点评 本题考查了等差数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
9.点M为圆P内不同于圆心的定点,过点M作圆Q与圆P相切,则圆心Q的轨迹是( )
| A. | 圆 | B. | 椭圆 | C. | 圆或线段 | D. | 线段 |
4.下列四个命题中,真命题是( )
| A. | 平面就是平行四边形 | |
| B. | 空间任意三点可以确定一个平面 | |
| C. | 两两相交的三条直线可以确定一个平面 | |
| D. | 空间四点不共面,则其中任意三点不共线 |
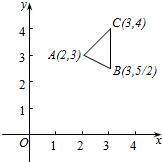 已知点(x,y)在△ABC所包围的阴影区域内(包含边界),若B是使得z=ax-y取得最大值的最优解,则实数a的取值范围为[-$\frac{1}{2}$,+∞).
已知点(x,y)在△ABC所包围的阴影区域内(包含边界),若B是使得z=ax-y取得最大值的最优解,则实数a的取值范围为[-$\frac{1}{2}$,+∞).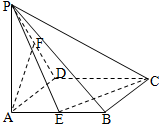 如图,四棱锥P-ABCD的底面为正方形,PA⊥底面ABCD,E、F分别为AB、PD的中点.
如图,四棱锥P-ABCD的底面为正方形,PA⊥底面ABCD,E、F分别为AB、PD的中点.