题目内容
如图,在底面是矩形的四棱锥P—ABCD中,PA⊥底面ABCD,PA=AB=1,BC=2.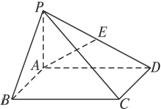
(1)求证:平面PDC⊥平面PAD;
(2)若E是PD的中点,求异面直线AE与PC所成角的余弦值;
(3)在BC边上是否存在一点G,使得D点到平面PAG的距离为1?若存在,求出BG的值;若不存在,请说明理由.
证明:以A为原点,AB所在直线为x轴,AD所在直线为y轴,AP所在直线为z轴建立空间直角坐标系,则A(0,0,0),B(1,0,0),C(1,2,0),D(0,2,0),E(0,1,![]() ),P(0,0,1).
),P(0,0,1).
∴![]() =(-1,0,0),
=(-1,0,0), ![]() =(0,2,0),
=(0,2,0),![]() =(0,0,1),
=(0,0,1), ![]() =(0,1,
=(0,1,![]() ),
), ![]() =(1,2,-1).
=(1,2,-1).
(1) 平面PDC⊥平面PAD.
平面PDC⊥平面PAD.
(2)∵cos〈![]() ,
,![]() 〉=
〉= =
= =
=![]() ,
,
∴所求角的余弦值为![]() .
.
(3)假设BC边上存在一点G满足题设条件,令BG=x(0≤x≤2),则G(1,x,0),作DQ⊥AG,垂足为Q,则DQ⊥平面PAG,即DQ=1.
∵2S△ADG=S矩形ABCD,
∴|![]() |·|
|·|![]() |=|
|=|![]() |·|
|·|![]() |=2.∴|
|=2.∴|![]() |=2.
|=2.
又AG=![]() ,∴x=
,∴x=![]() <2.
<2.
故存在点G,当BG=3时,使点D到平面PAG的距离为1.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
 (2012•惠州模拟)如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=2,E是PD的中点.
(2012•惠州模拟)如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=2,E是PD的中点.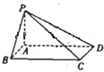 如图,在底面是矩形的四棱锥P-ABCD中,PA⊥底面ABCD,PA=AB=2,BC=4.
如图,在底面是矩形的四棱锥P-ABCD中,PA⊥底面ABCD,PA=AB=2,BC=4.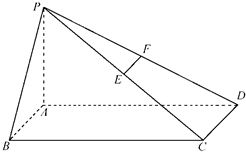 (2010•通州区一模)如图,在底面是矩形的四棱锥P-ABCD中,PA⊥底面ABCD,E、F分别是PC、PD的中点,求证:
(2010•通州区一模)如图,在底面是矩形的四棱锥P-ABCD中,PA⊥底面ABCD,E、F分别是PC、PD的中点,求证: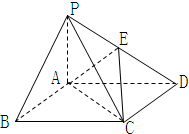 如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点
如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点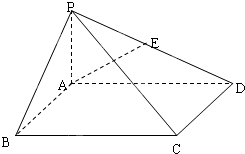 如图,在底面是矩形的四棱锥P-ABCD中,PA⊥面ABCD,PA=AB=1,BC=2.
如图,在底面是矩形的四棱锥P-ABCD中,PA⊥面ABCD,PA=AB=1,BC=2.