题目内容
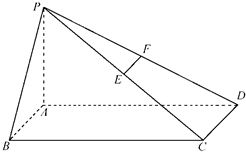 (2010•通州区一模)如图,在底面是矩形的四棱锥P-ABCD中,PA⊥底面ABCD,E、F分别是PC、PD的中点,求证:
(2010•通州区一模)如图,在底面是矩形的四棱锥P-ABCD中,PA⊥底面ABCD,E、F分别是PC、PD的中点,求证:(Ⅰ)EF∥平面PAB;
(Ⅱ)平面PAD⊥平面PDC.
分析:(I)由E、F分别是PC、PD的中点,可由三角形中位线定理得到EF∥CD,进而根据底面是矩形,对边平行得到EF∥AB,结合线面平行的判定定理得到EF∥平面PAB;
(Ⅱ)由PA⊥底面ABCD,底面ABCD是矩形,可得PA⊥CD及AD⊥CD,进而由线面垂直的判定定理得到DC⊥平面PAD,进而由面面垂直的判定定理得到平面PAD⊥平面PDC.
(Ⅱ)由PA⊥底面ABCD,底面ABCD是矩形,可得PA⊥CD及AD⊥CD,进而由线面垂直的判定定理得到DC⊥平面PAD,进而由面面垂直的判定定理得到平面PAD⊥平面PDC.
解答:证明: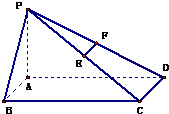 (Ⅰ)∵E、F分别是PC、PD的中点,
(Ⅰ)∵E、F分别是PC、PD的中点,
∴EF∥CD. (2分)
∵底面ABCD是矩形,
∴CD∥AB.
∴EF∥AB. (4分)
又AB?平面PAB,EF?平面PAB,
∴EF∥平面PAB. (7分)
(Ⅱ)∵PA⊥底面ABCD,CD?底面ABCD
∴PA⊥CD. (8分)
∵底面ABCD是矩形,AD⊥CD. (10分)
又PA∩AD=A,AP?面PAD,AD?面PAD,
∴DC⊥平面PAD. (12分)
∵DC?平面PDC,
∴平面PAD⊥平面PDC. (14分)
 (Ⅰ)∵E、F分别是PC、PD的中点,
(Ⅰ)∵E、F分别是PC、PD的中点,∴EF∥CD. (2分)
∵底面ABCD是矩形,
∴CD∥AB.
∴EF∥AB. (4分)
又AB?平面PAB,EF?平面PAB,
∴EF∥平面PAB. (7分)
(Ⅱ)∵PA⊥底面ABCD,CD?底面ABCD
∴PA⊥CD. (8分)
∵底面ABCD是矩形,AD⊥CD. (10分)
又PA∩AD=A,AP?面PAD,AD?面PAD,
∴DC⊥平面PAD. (12分)
∵DC?平面PDC,
∴平面PAD⊥平面PDC. (14分)
点评:本题考查的知识点是平面与平面垂直的判定,直线与平面平行的判定,其中(I)的关键是证得EF∥AB,(II)的关键是证得DC⊥平面PAD.

练习册系列答案
相关题目
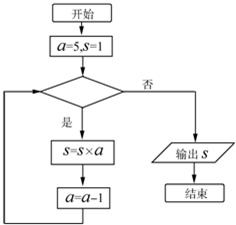 (2010•通州区一模)执行图所示的程序,输出的结果为20,则判断框中应填入的条件为( )
(2010•通州区一模)执行图所示的程序,输出的结果为20,则判断框中应填入的条件为( )
 (2010•通州区一模)设不等式组
(2010•通州区一模)设不等式组