题目内容
3.已知直线l:x=2和圆C:x2+y2-2x-2y=0,则圆C上到直线l的距离等于1的点的个数为1.分析 将圆方程化为标准方程,找出圆心坐标与半径,求出圆心到已知直线的距离,即可得出结论.
解答 解:圆方程变形得:(x-1)2+(y-1)2=2,即圆心(1,1),半径r=$\sqrt{2}$,
∴圆心到直线x=2的距离d=1<$\sqrt{2}$,r-d<1
∴圆C上到直线l的距离等于1的点的个数为2,
故答案为2.
点评 此题考查了直线与圆的位置关系,以及点到直线的距离公式,弄清题意是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.已知x,y∈(0,+∞),且满足$\frac{1}{x}+\frac{1}{2y}=2$,那么x+4y的最小值为( )
| A. | $\frac{3}{2}-\sqrt{2}$ | B. | $3+\frac{{\sqrt{2}}}{2}$ | C. | $\frac{3}{2}+\sqrt{2}$ | D. | $3-\frac{{\sqrt{2}}}{2}$ |
12.若x,y满足约束条件$\left\{\begin{array}{l}y≤x\\ x+y≤1\\ y≥-1\end{array}\right.$,则z=2x-y的最大值为( )
| A. | 5 | B. | 3 | C. | -1 | D. | $\frac{1}{2}$ |
19.已知全集U=R,集合A={x|x<1},则∁UA=( )
| A. | (-∞,1] | B. | [1,+∞) | C. | R | D. | (1,+∞) |
8.设a=log39,b=20.7,c=($\frac{1}{2}$)${\;}^{-\frac{2}{3}}$,则a,b,c的大小关系为( )
| A. | a>b>c | B. | b>a>c | C. | a>c>b | D. | c>a>b |
 ,那么 ( )
,那么 ( ) B.
B. C.
C. D.
D.
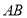 为圆锥
为圆锥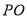 的底面直径,
的底面直径,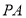 为母线,点
为母线,点 在底面圆周上,若
在底面圆周上,若 ,
,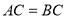 ,则二面角
,则二面角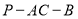 大小的正切值是( )
大小的正切值是( )
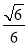 B.
B. C.
C.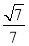 D.
D.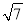
 中,角
中,角 所对的边分别为
所对的边分别为 ,已知
,已知 ,则
,则 .
.