��Ŀ����
12��Ϊ�˵���ס���������վ�ܻ�ӭ�ij̶ȣ����ѡȡ��14�죬ͳ������8��00-10��00����Եĵ���������������ݣ��ף�73��24��58��72��64��38��66��70��20��41��55��67��8��25��
�ң�12��37��21��5��54��42��61��45��19��6��19��36��42��14��
��1���þ�Ҷͼ��ʾ��������ݣ�
��2������վ�������[10��40]���Ƶ���Ƕ��٣�
��3����ͳ�ƵĽǶȿ��ǣ�����Ϊ�ĸ���վ���ܻ�ӭ����˵�����ɣ�
���� ��1��������Ŀ�е����ݣ�������Ҷͼ���ɣ�
��2������Ƶ����Ƶ�������������Ĺ�ϵ���㼴�ɣ�
��3�����ݾ�Ҷͼ�е����ݷֲ�����������ɣ�
��� �⣺��1��������Ŀ�е����ݣ�������Ҷͼ��ͼ��ʾ��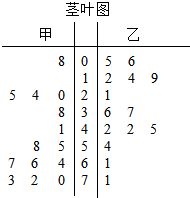
��2������վ�������[10��40]���Ƶ����3+1=4��
Ƶ����$\frac{4}{14}$=$\frac{2}{7}$��
��3�����ݾ�Ҷͼ֪��
����վ�ĵ���������ھ�Ҷͼ�·���
����վ�ĵ���������ھ�Ҷͼ�Ϸ���
�����ݵķֲ������������վ���ܻ�ӭ��
���� ���⿼���˾�Ҷͼ��Ӧ�����⣬����ʱӦ�����þ�Ҷͼ�������ݣ��ó�ͳ�ƽ��ۣ��ǻ����⣮

��ϰ��ϵ�д�
 ���Ž�������С״Ԫϵ�д�
���Ž�������С״Ԫϵ�д�
�����Ŀ
2����֪����f��x��=��$\frac{1}{3}$��x��a��0��b��0��a��b��m=f��$\frac{a+b}{2}$����n=f��$\sqrt{ab}$����p=f��$\frac{2ab}{a+b}$������m��n��p �Ĵ�С��ϵΪ��������
| A�� | m��n��p | B�� | m��p��n | C�� | p��m��n | D�� | p��n��m |
3����֪����$\overrightarrow{a}$=��cos�ȣ�sin�ȣ����ȡʣ�0���У���$\overrightarrow{b}$=��1��$\sqrt{3}$������$\overrightarrow{a}$��$\overrightarrow{b}$���ߣ���sin2��=��������
| A�� | $\frac{1}{2}$ | B�� | $\frac{\sqrt{3}}{2}$ | C�� | -$\frac{1}{2}$ | D�� | -$\frac{\sqrt{3}}{2}$ |
20����֪����f��x��=x2+bx+c��f��-1��=f��3����������
| A�� | f ��1����c��f ��-1�� | B�� | f ��1����c��f ��-1�� | C�� | c��f ��-1����f ��1�� | D�� | c��f ��-1����f ��1�� |
1����֪����Ǧ����ձ߾�����P��-3��m������cos��=-$\frac{3}{5}$����sin��=��������
| A�� | -$\frac{4}{5}$ | B�� | $\frac{4}{5}$ | C�� | ��$\frac{4}{5}$ | D�� | ��$\frac{3}{5}$ |