题目内容
在锐角△ABC中,已知角A、B、C所对的边分别为a,b,c,且tanA-tanB=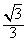 (1+tanAtanB),
(1+tanAtanB),
(1)若c2=a2+b2-ab,求角A、B、C的大小;
(2)已知向量m=(sinA,cosA),n=(cosB,sinB),求|3m-2n|的取值范围.
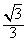 (1+tanAtanB),
(1+tanAtanB),(1)若c2=a2+b2-ab,求角A、B、C的大小;
(2)已知向量m=(sinA,cosA),n=(cosB,sinB),求|3m-2n|的取值范围.
解:(1)由已知得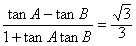 ,故
,故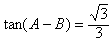 ,
,
又0<A,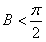 ,
,
从而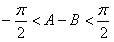 即
即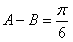 ,
,
由c2=a2+b2-ab得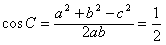 ,可得
,可得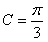 ,
,
由A+B+C=π,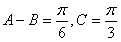 ,
,
可解得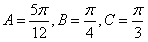 。
。
(2)|3m-2n|2=9|m|2-12m·n+4|n|2
=13-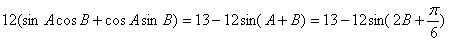 ,
,
由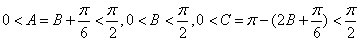 得
得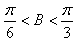 ,
,
从而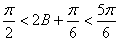 ,
,
故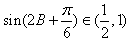 ,
,
即|3m-2n|∈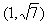 。
。
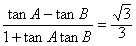 ,故
,故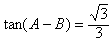 ,
,又0<A,
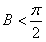 ,
,从而
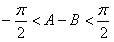 即
即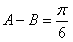 ,
,由c2=a2+b2-ab得
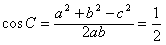 ,可得
,可得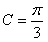 ,
,由A+B+C=π,
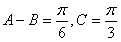 ,
,可解得
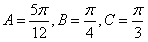 。
。(2)|3m-2n|2=9|m|2-12m·n+4|n|2
=13-
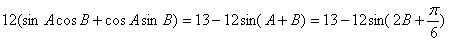 ,
,由
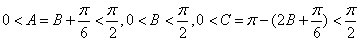 得
得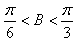 ,
,从而
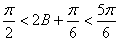 ,
,故
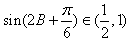 ,
,即|3m-2n|∈
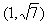 。
。
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目