题目内容
如图1-1-2所示,为处理含有某种杂质的污水,要制造一底宽为2 m的无盖长方体沉淀箱.污水从A孔流入,经沉淀后从B孔流出.设箱体的长度为a m,高度为b m.已知流出的水中该杂质的质量分数与a、b的乘积ab成反比.现有制箱材料60 m2,问当a、b各为多少时,经沉淀后流出的水中该杂质的质量分数最小(A、B孔的面积忽略不计).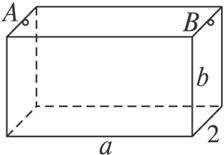
图1-1-2
分析:依题意可以建立两个基本的等量关系:①y=![]() (y为质量分数,k为比例系数);②4b+2ab+2a=60.具体求解可有两条思路:一是将②式变形代入①式消元成一元函数,再求使y取得最小值时的自变量值;二是由①式知y为最小值等价于求ab的最大值,将ab看作一个整体,利用②式去寻求.在求最值的过程中,若遇到变量的和式或积式可考虑运用均值定理.
(y为质量分数,k为比例系数);②4b+2ab+2a=60.具体求解可有两条思路:一是将②式变形代入①式消元成一元函数,再求使y取得最小值时的自变量值;二是由①式知y为最小值等价于求ab的最大值,将ab看作一个整体,利用②式去寻求.在求最值的过程中,若遇到变量的和式或积式可考虑运用均值定理.
解法一:设y为流出的水中杂质的质量分数,则y=![]() ,其中k>0为比例系数.
,其中k>0为比例系数.
根据题设,有
4b+2ab+2a=60(a>0,b>0),
∴b=![]() (0<a<30).③
(0<a<30).③
于是y=![]() =
= =
=
=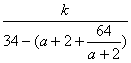
≥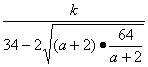 =
=![]() .
.
当a+2=![]() 时取等号,y达到最小值.
时取等号,y达到最小值.
这时a=6或a=-10(舍去).
将a=6代入③式得b=3.
当a为6 m,b为3 m时,经沉淀后流出的水中该杂质的质量分数最小.
解法二:设y为流出的水中杂质的质量分数,则y=![]() ,其中k>0为比例系数.
,其中k>0为比例系数.
依题意,即所求的a、b值使ab最大.
由题设,知4b+2ab+2a=60(a>0,b>0),
即a+2b+ab=30(a>0,b>0).
∵a+2b≥2![]() ,
,
∴2![]()
![]() +ab≤30
+ab≤30![]() ab+2
ab+2![]()
![]() -30≤0
-30≤0![]() (
(![]() +5
+5![]() )(
)(![]() -3
-3![]() )≤0.
)≤0.
当且仅当a=2b时,上式取等号.
当a>0,b>0时,解得0<ab≤18,
即当a=2b时,ab取得最大值为18.
∴2b2=18.解得b=3,则a=6.
故当a为6 m,b为3 m时,经沉淀后流出的水中该杂质的质量分数最小.

练习册系列答案
相关题目
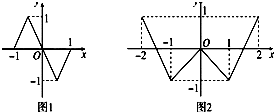 (2012•唐山二模)奇函数f(x)、偶函数g(x)的图象分别如图1、2所示,方程f(g(x))=0、g(f(x))=0的实根个数分别为a、b,则a+b=( )
(2012•唐山二模)奇函数f(x)、偶函数g(x)的图象分别如图1、2所示,方程f(g(x))=0、g(f(x))=0的实根个数分别为a、b,则a+b=( ) (2013•海淀区二模)如图1,在直角梯形ABCD中,∠ABC=∠DAB=90°,∠CAB=30°,BC=2,AD=4.把△DAC沿对角线AC折起到△PAC的位置,如图2所示,使得点P在平面ABC上的正投影H恰好落在线段AC上,连接PB,点E,F分别为线段PA,PB的中点.
(2013•海淀区二模)如图1,在直角梯形ABCD中,∠ABC=∠DAB=90°,∠CAB=30°,BC=2,AD=4.把△DAC沿对角线AC折起到△PAC的位置,如图2所示,使得点P在平面ABC上的正投影H恰好落在线段AC上,连接PB,点E,F分别为线段PA,PB的中点. 、偶函数
、偶函数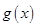 的图象分别如图1、2所示,方程
的图象分别如图1、2所示,方程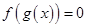 ,
,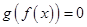 的实根个数分别为
的实根个数分别为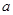 、
、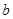 ,则
,则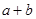 等于( )
等于( )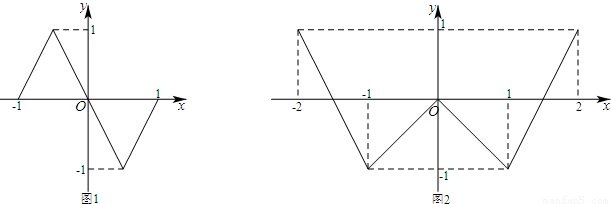
 B.
B.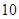 C.
C.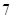 D.
D.