题目内容
【题目】已知关于
的不等式
的解集为
.
（1）若
是从
四个数中任取的一个数， 
是从
三个数中任取的一个数，求
不为空集的概率；
（2）若
是从区间
上任取的一个数， 
是从区间
上任取的一个数，求
不为空集的概率.
【答案】（1）
；（2）
.
【解析】试题分析：（1）根据题意，“
不为空集”等价于“不等式
有解”，即方程
有实根，所以
，即
，又
是从
， 
， 
， 
四个数中任取的一个数， 
是从
， 
， 
三个数中任取的一个数，因此基本事件共有
个，其中
， 
， 
， 
， 
， 
， 
， 
， 
满足条件，则
；（2）根据题意，试验的全部结果构成的区域为
，满足题意的区域为
，从而可得所求概率为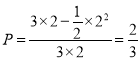
.
试题解析：方程有实根的充要条件为
，即
，……………………1分
（1）基本事件共有12个，其中
， 
满足条件，则
.………………………………………………5分
（2）试验的全部结果构成的区域为
，………………………………7分
满足题意的区域为
，……………………………………9分
所以，所求概率为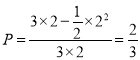
.……………………………………12分
练习册系列答案
相关题目
【题目】某校100名学生期中考试数学成绩的频率分布直方图如图，其中成绩分组区间如下：
组号 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 |
分组 |
|
|
|
|
|
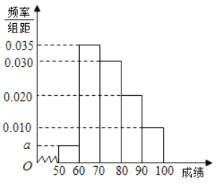
（1）求图中
的值；
（2）根据频率分布直方图，估计这100名学生期中考试数学成绩的平均分；
（3）现用分层抽样的方法从第3、4、5组中随机抽取6名学生，将该样本看成一个总体，从中随机抽取2名，求其中恰有1人的分数不低于90分的概率？
