题目内容
已知动圆C过定点F( ),且与直线x=
),且与直线x= 相切,圆心C的轨迹记为E.,曲线E与直线l:y=k(x+1)(k∈R)相交于A、B两点.
相切,圆心C的轨迹记为E.,曲线E与直线l:y=k(x+1)(k∈R)相交于A、B两点.(Ⅰ)求曲线E的方程;
(Ⅱ)当△OAB的面积等于
 时,求k的值;
时,求k的值;(Ⅲ)在曲线E上,是否存在与k的取值无关的定点M,使得MA⊥MB?若存在,求出所有符合条件的定点M;若不存在,请说明理由.
【答案】分析:(Ⅰ)由抛物线的定义易知这是一条以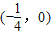 为焦点,以x=
为焦点,以x= 为准线的抛物线,即可得其标准方程
为准线的抛物线,即可得其标准方程
(Ⅱ)将直线与曲线联立,利用韦达定理,设而不求,将△OAB的面积表示为k的函数,求最值即可
(Ⅲ)假设存在这样的点,由MA⊥MB,得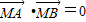 ,再结合(Ⅱ)中的结论即可求得此定点
,再结合(Ⅱ)中的结论即可求得此定点
解答: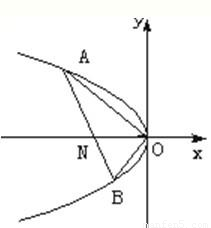 解:(Ⅰ)点C的轨迹方程为y2=-x,
解:(Ⅰ)点C的轨迹方程为y2=-x,
(Ⅱ).由方程组
消去x后,整理得
y2=-x,
y=k(x+1)
ky2+y-k=0.
设A(x1,y1)、B(x2,y2),由韦达定理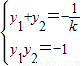
∵A、B在抛物线y2=-x上,
∴y12=-x1,y22=-x2,y12•y22=x1x2.
设直线l与x轴交于点N,则N(-1,0)
∵S△OAB=S△OAN+S△OBN
= |ON||y1|+
|ON||y1|+ |ON||y2|
|ON||y2|
= |ON|•|y1-y2|,
|ON|•|y1-y2|,
∴S△OAB= •1•
•1•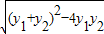
=
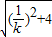
∵S△OAB=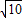 ,
,
∴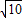 =
=
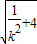 .解得k=±
.解得k=±
(Ⅲ)设点M(x,y),若(y1-y)(y2-y)+(x1-x)(x2-x)=0
?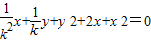
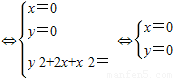
故存在唯一的合乎题意的点M(0,0)
点评:本题综合考查了抛物线的定义和标准方程,直线与抛物线的关系,解题时要耐心细致,准确作答
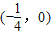 为焦点,以x=
为焦点,以x= 为准线的抛物线,即可得其标准方程
为准线的抛物线,即可得其标准方程(Ⅱ)将直线与曲线联立,利用韦达定理,设而不求,将△OAB的面积表示为k的函数,求最值即可
(Ⅲ)假设存在这样的点,由MA⊥MB,得
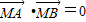 ,再结合(Ⅱ)中的结论即可求得此定点
,再结合(Ⅱ)中的结论即可求得此定点解答:
 解:(Ⅰ)点C的轨迹方程为y2=-x,
解:(Ⅰ)点C的轨迹方程为y2=-x,(Ⅱ).由方程组
消去x后,整理得
y2=-x,
y=k(x+1)
ky2+y-k=0.
设A(x1,y1)、B(x2,y2),由韦达定理
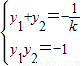
∵A、B在抛物线y2=-x上,
∴y12=-x1,y22=-x2,y12•y22=x1x2.
设直线l与x轴交于点N,则N(-1,0)
∵S△OAB=S△OAN+S△OBN
=
 |ON||y1|+
|ON||y1|+ |ON||y2|
|ON||y2|=
 |ON|•|y1-y2|,
|ON|•|y1-y2|,∴S△OAB=
 •1•
•1•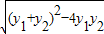
=

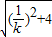
∵S△OAB=
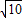 ,
,∴
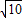 =
=
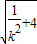 .解得k=±
.解得k=±
(Ⅲ)设点M(x,y),若(y1-y)(y2-y)+(x1-x)(x2-x)=0
?
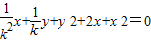
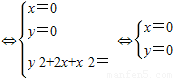
故存在唯一的合乎题意的点M(0,0)
点评:本题综合考查了抛物线的定义和标准方程,直线与抛物线的关系,解题时要耐心细致,准确作答

练习册系列答案
相关题目
 ),且与直线x=
),且与直线x= 相切,圆心C的轨迹记为E.,曲线E与直线l:y=k(x+1)(k∈R)相交于A、B两点.
相切,圆心C的轨迹记为E.,曲线E与直线l:y=k(x+1)(k∈R)相交于A、B两点. 时,求k的值;
时,求k的值;