题目内容
已知方程x2-2ax-b2+16=0(a,b∈R).
(1)若a,b分别是一枚骰子掷两次所得到的点数,求方程有两个不同正根的概率;
(2)若a∈[0,6],b∈[0,4],求方程没有实根的概率.
(1)若a,b分别是一枚骰子掷两次所得到的点数,求方程有两个不同正根的概率;
(2)若a∈[0,6],b∈[0,4],求方程没有实根的概率.
考点:几何概型
专题:计算题,概率与统计
分析:(1)这是一个古典概型问题,总件数由分步计数原理知是36,满足条件的事件数在整理时要借助于根与系数之间的关系,根的判别式,要进行讨论得到结果;
(2)本题是一个几何概型,试验的全部结果构成区域Ω={(a,b)|0≤a≤6,0≤b≤4},满足条件的事件为:B={(a,b)|0≤a≤6,0≤b≤4,a2+b2<16},做出两者的面积,得到概率.
(2)本题是一个几何概型,试验的全部结果构成区域Ω={(a,b)|0≤a≤6,0≤b≤4},满足条件的事件为:B={(a,b)|0≤a≤6,0≤b≤4,a2+b2<16},做出两者的面积,得到概率.
解答:
解:(1)基本事件(a,b)共有36个,方程有不同正根等价于
⇒
设“方程有两个不同正根”为事件A,则事件A包含的基本事件为(6,1),(6,2),(6,3),(5,1),(5,2),(5,3),(4,1),(4,2),(4,3),(3,3),共10个,
故所求的概率为P(A)=
=
.6分
(2)试验的全部结果构成区域Ω={(a,b)|0≤a≤6,0≤b≤4},其面积为S(Ω)=24,
设“方程无实根”为事件B,则构成事件B的区域为B={(a,b)|0≤a≤6,0≤b≤4,a2+b2<16},
其面积为S(B)=
×π×42=4π,
故所求的概率为P(B)=
=
.12分.
|
|
设“方程有两个不同正根”为事件A,则事件A包含的基本事件为(6,1),(6,2),(6,3),(5,1),(5,2),(5,3),(4,1),(4,2),(4,3),(3,3),共10个,
故所求的概率为P(A)=
| 10 |
| 36 |
| 5 |
| 18 |
(2)试验的全部结果构成区域Ω={(a,b)|0≤a≤6,0≤b≤4},其面积为S(Ω)=24,
设“方程无实根”为事件B,则构成事件B的区域为B={(a,b)|0≤a≤6,0≤b≤4,a2+b2<16},
其面积为S(B)=
| 1 |
| 4 |
故所求的概率为P(B)=
| 4π |
| 24 |
| π |
| 6 |
点评:本题考查古典概型和几何概型,解决古典概型问题时,先要判断该概率模型是不是古典概型,再要找出随机事件A包含的基本事件的个数和试验中基本事件的总数.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
设集合A={x|ln(1-x)>0},B={x|-1≤x≤1},则A∩B=( )
| A、[-1,0] |
| B、(-1,0) |
| C、[-1,0) |
| D、(-1,1) |
等比数列{an}中,首项a1=2,公比为3,Sn为其前n项和,则S4+a3等于( )
| A、44 | B、64 | C、98 | D、134 |
函数y=
的大致图象只能是( )
| 1 |
| x+2 |
A、 |
B、 |
C、 |
D、 |
△ABC中,cosAcosBcosC的最大值是( )
A、
| ||||
B、
| ||||
| C、1 | ||||
D、
|
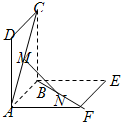 如图,已知四边形ABCD,ABEF都是矩形,M、N分别是对角线AC和BF的中点,则MN与平面BCE的关系是
如图,已知四边形ABCD,ABEF都是矩形,M、N分别是对角线AC和BF的中点,则MN与平面BCE的关系是