题目内容
过抛物线y2=2px（p＞0）的对称轴上一点A（a，0）的直线与抛物线相交于M、N两点，自M、N向直线l：x=-a作垂线，垂足分别为M1、N1。
（1）当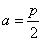
时，求证：AM1⊥AN1；
（2）记△AMM1、△AM1N1、△ANN1的面积分别为S1、S2、S3，是否存在λ，使得对任意的a＞0，都有S22=λS1S2成立。若存在，求出λ的值；若不存在，说明理由
（1）当
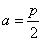时，求证：AM1⊥AN1；（2）记△AMM1、△AM1N1、△ANN1的面积分别为S1、S2、S3，是否存在λ，使得对任意的a＞0，都有S22=λS1S2成立。若存在，求出λ的值；若不存在，说明理由
解：依题意，可设直线MN的方程为 ， ，则有 由  消去x可得 从而有  ①于是  ②又由  ， ，可得 ③ |
|
（1）如图，当 时，点 即为抛物线的焦点，l为其准线 此时  ，并由①可得 ∵  ∴  即  。 |
 |
（2）存在 ，使得对任意的 ，都有成立 ，证明如下：记直线l与x轴的交点为A1，则  。于是有    ∴   将①、②、③代入上式化简可得  上式恒成立，即对任意  成立。 |
练习册系列答案
相关题目
过抛物线y2=2px（p＞0）的焦点F的直线l与抛物线在第一象限的交点为A，与抛物线的准线的交点为B，点A在抛物线准线上的射影为C，若
=
，
•
=48，则抛物线的方程为（ ）
| AF |
| FB |
| BA |
| BC |
| A、y2=4x | ||
| B、y2=8x | ||
| C、y2=16x | ||
D、y2=4
|
过抛物线y2=2px（p＞0）的焦点F作直线交抛物线于A、B两点，O为抛物线的顶点．则△ABO是一个（ ）
| A、等边三角形 | B、直角三角形 | C、不等边锐角三角形 | D、钝角三角形 |