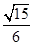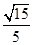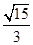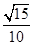题目内容
设四面体的六条棱的长分别为1,1,1,1,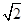 和
和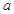 ,且长为
,且长为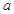 的棱与长为
的棱与长为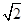 的棱异面,则
的棱异面,则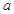 的取值范围是
的取值范围是
A.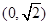 | B.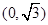 | C.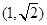 | D.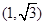 |
A
解析试题分析:设四面体的底面是BCD,BC=a,BD=CD=1,顶点为A,AD=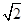 ,在三角形BCD中,因为两边之和大于第三边可得:0<a<2 …………………………①
,在三角形BCD中,因为两边之和大于第三边可得:0<a<2 …………………………①
取BC中点E,∵E是中点,△ACE≌△DCE,所以在△AED中,AE=ED= ,因为两边之和大于第三边,所以
,因为两边之和大于第三边,所以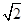 <2
<2 ,即0<a<
,即0<a<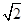 ……………………②
……………………②
由①②得: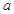 的取值范围是
的取值范围是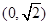 ,故选:A。
,故选:A。
考点:异面直线的判定;棱锥的结构特征;
点评:本题主要考察三角形三边关系以及异面直线的位置.解决本题的关键在于利用三角形两边之和大于第三边这一结论。

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
设有一几何体的三视图如下,则该几何体体积为( )

正视图 侧视图
俯视图(圆和正方形)
A.4+ | B.4+ | C.4+ | D.4+ |
已知a、b是异面直线,直线c//a,那么c与b ( )
| A.一定是异面直线 | B.一定是相交直线 |
| C.不可能是相交直线 | D.不可能是平行直线 |
一个棱锥的三视图如图,则该棱锥的全面积(单位:cm2)为( ) 
A.36+12 | B.48+24 | C.48+12 | D.36+24 |
正三棱柱 的各棱长都是2,E,F分别是
的各棱长都是2,E,F分别是 的中点,则EF的长是( )
的中点,则EF的长是( )
| A.2 | B. | C. | D. |





 与
与 是异面直线的是 ……………………………………………( )
是异面直线的是 ……………………………………………( )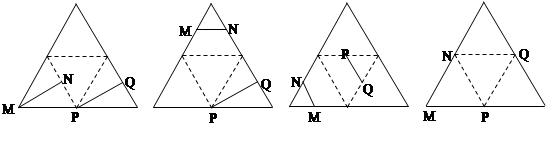
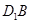 所成角的余弦值为()
所成角的余弦值为()