题目内容
解析：(1)当0＜x≤10时，f(x)＝－0.1x2＋2.6x＋43＝－0.1(x－13)2＋59.9
故f(x)在0＜x≤10时递增，最大值为f(10)＝－0.1(10－13)2＋59.9＝59
当10＜x≤16时，f(x)≡59
当x＞16时，f(x)为减函数，且f(x)＜59
因此，开讲10分钟后，学生达到最强接受能力(为59)，能维持6分钟时间.…………5分
(2)f(5)＝－0.1(5－13)2＋59.9＝53.5
f(20)＝－3×20＋107＝47＜53.5
故开讲5分钟时学生的接受能力比开讲20分钟时要强一些.……………………………8分
(3)当0＜x≤10时，令f(x)＝55，解得x＝6或20(舍)
当x＞16时，令f(x)＝55，解得x＝17
因此学生达到(含超过)55的接受能力的时间为17－6＝11＜13(分)
老师来不及在学生一直达到所需接受能力的状态下讲授完这个难题.。。。。。。。。。。。。14分
故f(x)在0＜x≤10时递增，最大值为f(10)＝－0.1(10－13)2＋59.9＝59
当10＜x≤16时，f(x)≡59
当x＞16时，f(x)为减函数，且f(x)＜59
因此，开讲10分钟后，学生达到最强接受能力(为59)，能维持6分钟时间.…………5分
(2)f(5)＝－0.1(5－13)2＋59.9＝53.5
f(20)＝－3×20＋107＝47＜53.5
故开讲5分钟时学生的接受能力比开讲20分钟时要强一些.……………………………8分
(3)当0＜x≤10时，令f(x)＝55，解得x＝6或20(舍)
当x＞16时，令f(x)＝55，解得x＝17
因此学生达到(含超过)55的接受能力的时间为17－6＝11＜13(分)
老师来不及在学生一直达到所需接受能力的状态下讲授完这个难题.。。。。。。。。。。。。14分
练习册系列答案
相关题目
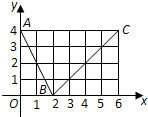如图，函数f（x）的图象是折线段ABC，其中A，B，C的坐标分别为（0，4），（2，0），（6，4），则f（f（0））=