题目内容
8.若f(x)在R上为减函数,且f(-x)=-f(x),f(m-1)+f(2m-1)>0,求m的取值范围.分析 利用函数的奇偶性以及函数的单调性列出不等式求解即可.
解答 解:f(x)在R上为减函数,且f(-x)=-f(x),
f(m-1)+f(2m-1)>0,
可得f(m-1)>f(1-2m).
化为:m-1<1-2m,
解得m<$\frac{2}{3}$.
m的取值范围:($\frac{2}{3}$,+∞).
点评 本题考查函数的单调性以及奇偶性的应用,考查计算能力.

练习册系列答案
相关题目
19.下面说法错误的是( )
| A. | 数乘向量就是一个实数λ与向量$\overrightarrow{a}$的乘积 | |
| B. | λ>0,λ$\overrightarrow{a}$就是把$\overrightarrow{a}$同方向放大或缩小 | |
| C. | λ$\overrightarrow{a}$就是把$\overrightarrow{a}$沿反方向放大或缩小 | |
| D. | λ=0,则$λ\overrightarrow{a}$=$\overrightarrow{0}$ |
13.已知一次函数f(x)=ax+b,满足f(2)=0,f(-2)=1,则f(4)=( )
| A. | $\sqrt{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | 1 |
18.设A,B,C三个集合,为使A?(B∪C),条件A?B是( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
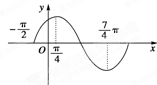 函数f(x)=sin(ωx+φ),(|φ|<$\frac{π}{2}$)的图象如图所示.试求:
函数f(x)=sin(ωx+φ),(|φ|<$\frac{π}{2}$)的图象如图所示.试求: