题目内容
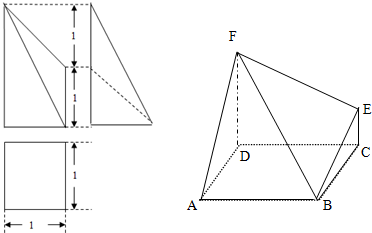
9.某几何体的三视图如图所示,则该几何体的表面积与体积比为( )
| A. | $3\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | 2$\sqrt{2}$+1 | D. | $\frac{{3\sqrt{2}}}{2}$ |
分析 由三视图可知:该几何体是由同底的上下两个圆锥组成的,分别利用表面积与体积计算公式即可得出.
解答 解:由三视图可知:该几何体是由同底的上下两个圆锥组成的,
∴该几何体的表面积与体积比=$\frac{2×\frac{1}{2}×2π×1×\sqrt{2}}{2×\frac{1}{3}×π×{1}^{2}×1}$=3$\sqrt{2}$.
故选:A.
点评 本题考查了圆锥的三视图、表面积与体积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
4.若A,B,C是函数f(x)=ex+x图象上横坐标成等差数列的三个点,给出以下判断:①△ABC可能是直角三角形;②△ABC一定是钝角三角形;③△ABC可能是等腰三角形;④△ABC一定不是等腰三角形.其中,正确的判断是( )
| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
20.已知函数f(x)对?x∈R都有f(x)=f(4-x),且其导函数f′(x)满足当x≠2时,(x-2)f′(x)>0,则当2<a<4时,有( )
| A. | f(2a)<f(2)<f(log2a) | B. | f(2)<f(2a)<f(log2a) | C. | f(log2a)<f(2a)<f(2) | D. | f(2)<f(log2a)<f(2a) |
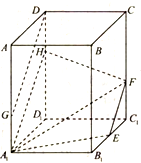 在正四棱柱ABCD-A1B1C1D1中,AB=2,AA1=3,E为B1C1的中点,F在CC1上,且C1F=1,G在AA1上,且AG=2.
在正四棱柱ABCD-A1B1C1D1中,AB=2,AA1=3,E为B1C1的中点,F在CC1上,且C1F=1,G在AA1上,且AG=2.