题目内容
设函数 。
。
(1)求函数 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(2)求函数 在区间
在区间 上的最小值和最大值,并求出取最值时
上的最小值和最大值,并求出取最值时 的值。
的值。
(1)最小正周期为 ,单调递增区间为
,单调递增区间为 ;(2)
;(2) 时,最小值-1,
时,最小值-1, 时,最大值
时,最大值 .
.
解析试题分析:(1)函数 的最小正周期是
的最小正周期是 ,求它的单调区间实质是借助整体法利用
,求它的单调区间实质是借助整体法利用 的单调区间,只不过要注意
的单调区间,只不过要注意 和
和 的正负;(2)求函数
的正负;(2)求函数 的最值也是利用整体思想,同样是借助于
的最值也是利用整体思想,同样是借助于 的最值.
的最值.
试题解析:(1) , 3分
, 3分
由 , 2分
, 2分
得 , 1分
, 1分
∴递增区间是 . 1分
. 1分
(2)令 ,则由
,则由 可得
可得 , 2分
, 2分
∴当 即
即 时,
时, . 2分
. 2分
当 即
即 时,
时, . 2分
. 2分
考点:(1)三角函数的最小正周期与单调区间;(2)在给定区间上的最值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (
( )的最小正周期为
)的最小正周期为 .求函数
.求函数 的单调增区间;
的单调增区间; 中,角
中,角 对边分别是
对边分别是 ,且满足
,且满足 .若
.若 ,
, .求角
.求角 的大小和边b的长.
的大小和边b的长.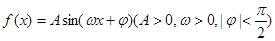 的图象的一部分如下图所示.
的图象的一部分如下图所示.
 的解析式;
的解析式; 时,求函数
时,求函数 的最大值与最小值及相应的
的最大值与最小值及相应的 的值.
的值.
 中,角
中,角 的对边分别为
的对边分别为 ,
, .
. 的大小;
的大小;
 的值域
的值域 .
. 的最小正周期;
的最小正周期; 上的函数值的取值范围.
上的函数值的取值范围. 函数
函数 .
. 的最小正周期及单调递减区间;
的最小正周期及单调递减区间; 的对边分别是
的对边分别是 ,且满足
,且满足 求
求 的取值范围.
的取值范围. .
. 的最小正周期;
的最小正周期; 时,求实数
时,求实数 的值,使函数
的值,使函数 并求此时
并求此时 上的对称中心.
上的对称中心.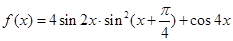 .
. 的最小正周期;
的最小正周期; 在
在 处取得最大值,求
处取得最大值,求 的值;
的值; 的单调递增区间.
的单调递增区间.