题目内容
设复数![]() 满足
满足![]() ,且
,且![]() 在复平面上对应的点在第二、四象限的角平分线上,若
在复平面上对应的点在第二、四象限的角平分线上,若![]() ,求
,求![]() 和
和![]() 的值。
的值。
![]() 或
或![]() ;
;![]() 或
或![]()
解析:
设![]() ,由
,由![]() ,得
,得![]()
![]()
又因为![]() 在复平面上对应的点在第二、四象限的角平分线上
在复平面上对应的点在第二、四象限的角平分线上
所以,![]() ,得
,得![]()
由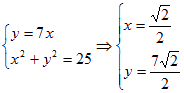 或
或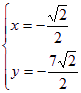
即![]() 或
或![]()
当![]() 时,由
时,由![]() ,即
,即![]() ,得
,得![]() 或
或![]()
当![]() 时,由
时,由![]() ,即
,即![]() ,得
,得![]() 或
或![]()
故![]() 或
或![]() ;
;![]() 或
或![]() ;
;

练习册系列答案
相关题目
题目内容
设复数![]() 满足
满足![]() ,且
,且![]() 在复平面上对应的点在第二、四象限的角平分线上,若
在复平面上对应的点在第二、四象限的角平分线上,若![]() ,求
,求![]() 和
和![]() 的值。
的值。
![]() 或
或![]() ;
;![]() 或
或![]()
设![]() ,由
,由![]() ,得
,得![]()
![]()
又因为![]() 在复平面上对应的点在第二、四象限的角平分线上
在复平面上对应的点在第二、四象限的角平分线上
所以,![]() ,得
,得![]()
由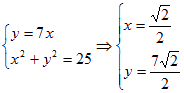 或
或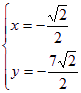
即![]() 或
或![]()
当![]() 时,由
时,由![]() ,即
,即![]() ,得
,得![]() 或
或![]()
当![]() 时,由
时,由![]() ,即
,即![]() ,得
,得![]() 或
或![]()
故![]() 或
或![]() ;
;![]() 或
或![]() ;
;
