Question

【题目】在四棱锥S-ABCD中，底面ABCD是边长为1的正方形，SD底面ABCD,SD=2，其中分别是的中点，是上的一个动点．

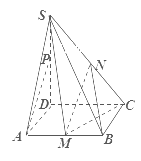
(1)当点落在什么位置时，∥平面，证明你的结论；

(2)求三棱锥的体积．

Answer 1

【答案】（1）当点为的中点时，∥平面。证明见解析；（2）。

【解析】

（1）当点P为SD的中点时，AP∥平面SMC，证明如下：连接PN，证明PN∥DC且，推出AM∥DC且，得到AP∥MN然后证明AP∥平面SMC．

（2）求出点N到平面ABCD的距离为h=1，然后求解三棱锥B﹣NMC的体积．

(1)当点为的中点时，∥平面。证明如下：

由三视图知该多面体是四棱锥，其底面边长为的正方形，侧棱底面，

且．

连接，

∵分别是的中点，

∴∥且，

又是正方形的边的中点，

∴∥且，

∴∥且，即四边形是平行四边形，

∴∥，又平面，平面，

∴∥平面．

(2)∵点到平面的距离为，∴点到平面的距离为，

∵三棱锥的体积满足：

.