题目内容
【题目】已知双曲线![]() 具有性质:若
具有性质:若![]() 、
、![]() 是双曲线左、右顶点,
是双曲线左、右顶点,![]() 为双曲线上一点,且
为双曲线上一点,且![]() 在第一象限.记直线
在第一象限.记直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,那么
,那么![]() 与
与![]() 之积是与点
之积是与点![]() 位置无关的定值.
位置无关的定值.
(1)试对椭圆![]() ,类比写出类似的性质(不改变原有命题的字母次序),并加以证明.
,类比写出类似的性质(不改变原有命题的字母次序),并加以证明.
(2)若椭圆![]() 的左焦点
的左焦点![]() ,右准线为
,右准线为![]() ,在(1)的条件下,当
,在(1)的条件下,当![]() 取得最小值时,求
取得最小值时,求![]() 的垂心
的垂心![]() 到
到![]() 轴的距离.
轴的距离.
【答案】(1)见解析(2) ![]() .
.
【解析】
(1)根据类比对应得椭圆性质,再根据斜率公式证结论,(2)先求得椭圆方程,再根据基本不等式确定最值取法,即得直线![]() 方程,与椭圆方程联立解得
方程,与椭圆方程联立解得![]() 点坐标,再根据直线
点坐标,再根据直线![]() 交点得垂心
交点得垂心![]() 坐标,即得结果.
坐标,即得结果.
(1)若![]() 、
、![]() 是椭圆
是椭圆![]() 左、右顶点,
左、右顶点,![]() 为椭圆
为椭圆![]() 上一点,且
上一点,且![]() 在第一象限.记直线
在第一象限.记直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,那么
,那么![]() 与
与![]() 之积是与点
之积是与点![]() 位置无关的定值,即
位置无关的定值,即![]() ;
;
证明如下:设![]()
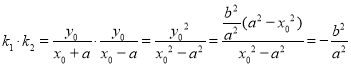
(2)因为椭圆![]() 的左焦点
的左焦点![]() ,右准线为
,右准线为![]() ,
,
所以![]() ,椭圆
,椭圆![]()
由(1)知![]() ,所以
,所以![]()
当且仅当![]() 即
即![]() 时取“
时取“![]() ”
”
此时直线![]() :
:![]()
与椭圆![]() 联立得
联立得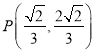
可设垂心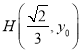 ,
,
由![]() ,故
,故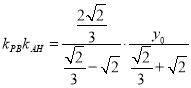
![]()
![]() 的垂心
的垂心![]() 到
到![]() 轴的距离为
轴的距离为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
