题目内容
△ABC中,BC=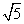 ,AC=3,sinC=2sinA。
,AC=3,sinC=2sinA。
(1)求AB的值;
(2)求sin(2A-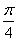 )。
)。
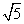 ,AC=3,sinC=2sinA。
,AC=3,sinC=2sinA。(1)求AB的值;
(2)求sin(2A-
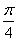 )。
)。解:(1)在△ABC中,根据正弦定理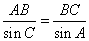
于是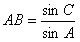 ·
·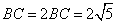 ;
;
(2)在△ABC中,根据余弦定理得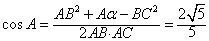
于是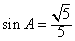
由倍角公式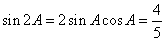
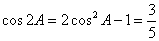
所以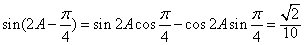 。
。
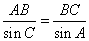
于是
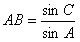 ·
·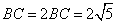 ;
;(2)在△ABC中,根据余弦定理得
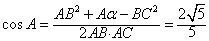
于是
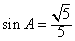
由倍角公式
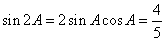
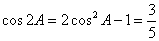
所以
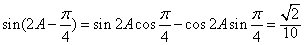 。
。
练习册系列答案
相关题目
题目内容
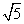 ,AC=3,sinC=2sinA。
,AC=3,sinC=2sinA。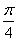 )。
)。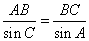
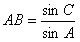 ·
·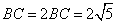 ;
;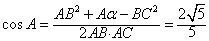
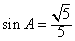
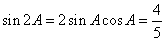
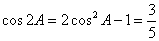
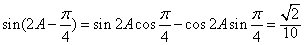 。
。