题目内容
15.已知sinα=-$\frac{2}{3}$,且α∈(-$\frac{π}{2}$,0),则tan(2π-α)的值为( )| A. | -$\frac{2\sqrt{5}}{5}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | ±$\frac{2\sqrt{5}}{5}$ | D. | $\frac{\sqrt{5}}{2}$ |
分析 由题意和同角三角函数基本关系可得cosα,再由诱导公式和同角三角函数基本关系可得.
解答 解:∵sinα=-$\frac{2}{3}$,且α∈(-$\frac{π}{2}$,0),
∴cosα=$\sqrt{1-si{n}^{2}α}$=$\frac{\sqrt{5}}{3}$,
∴tan(2π-α)=-tanα=-$\frac{sinα}{cosα}$=$\frac{2\sqrt{5}}{5}$,
故选:B.
点评 本题考查三角函数化简求值,涉及同角三角函数基本关系和诱导公式,属基础题.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
5.连锁水果店店主每天以每件50元购进水果若干件,以80元一件销售;若供大于求,当天剩余水果以40元一件全部退回;若供不应求,则立即从连锁店60元一件调剂,以80元一件销售.
(1)若水果店一天购进水果5件,求当天的利润y(单位:元)关于当天需求量n(单位:件,n∈N*)的函数解析式;
(2)店主记录了30天水果的日需求量n(单位:件)整理得表:
若水果店一天购进5件水果,以30天记录的各需求量发生的频率作为概率,求每天的利润在区间[150,200]的概率.
(1)若水果店一天购进水果5件,求当天的利润y(单位:元)关于当天需求量n(单位:件,n∈N*)的函数解析式;
(2)店主记录了30天水果的日需求量n(单位:件)整理得表:
| 日需求量 | 3 | 4 | 5 | 6 | 7 |
| 频数 | 2 | 3 | 15 | 6 | 4 |
6.设$\overrightarrow{a}$,$\overrightarrow{b}$均为非零向量,则“$\overrightarrow{a}$∥$\overrightarrow{b}$”是“$\overrightarrow{a}$与$\overrightarrow{b}$的方向相同”的( )
| A. | 充要条件 | B. | 充分但不必要条件 | ||
| C. | 必要但不充分条件 | D. | 既不充分也不必要条件 |
3.函数f(x)的定义域为R,“f(x)是奇函数”是“存在x∈R,f(x)+f(-x)=0”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
10.下列四个结论:
①若p∧q是真命题,则¬p可能是真命题;
②命题“?x0∈R,x02-x0-1<0”的否定是“?x∈R,x2-x-1≥0”;
③“a>5且b>-5”是“a+b>0”的充要条件;
④当a<0时,幂函数y=xa在区间(0,+∞)上单调递减.
其中正确结论的个数是( )
①若p∧q是真命题,则¬p可能是真命题;
②命题“?x0∈R,x02-x0-1<0”的否定是“?x∈R,x2-x-1≥0”;
③“a>5且b>-5”是“a+b>0”的充要条件;
④当a<0时,幂函数y=xa在区间(0,+∞)上单调递减.
其中正确结论的个数是( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
20.设i为虚数单位,则复数3-i的虚部是( )
| A. | 3 | B. | -i | C. | 1 | D. | -1 |
4.若函数y=f(x)的导函数为y=f′(x),且f′(x)=sin2x-$\sqrt{3}$cos2x,则下列说法正确的是( )
| A. | y=f(x)的周期为$\frac{π}{2}$ | B. | y=f(x)在[0,$\frac{π}{6}$]上是减函数 | ||
| C. | y=f(x)的图象关于直线x=$\frac{π}{2}$对称 | D. | y=f(x)是偶函数 |
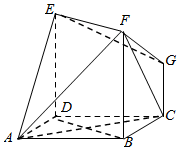 如图,矩形BDEF垂直于正方形ABCD,GC垂直于平面ABCD,且AB=DE=2CG=2.
如图,矩形BDEF垂直于正方形ABCD,GC垂直于平面ABCD,且AB=DE=2CG=2.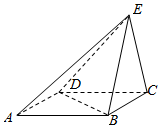 如图,ABCD是平行四边形,已知AB=2BC=4,BD=2$\sqrt{3}$,BE=CE,平面BCE⊥平面ABCD.
如图,ABCD是平行四边形,已知AB=2BC=4,BD=2$\sqrt{3}$,BE=CE,平面BCE⊥平面ABCD.