题目内容
椭圆
的离心率
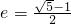，左顶点为A，右焦点为F，上顶点为B，则直线AB与FB的夹角θ=________．
90°
分析：把直线AB与FB的夹角看做向量
与向量
的夹角，分别求出两个向量的坐标，代入向量的数量积公式，利用椭圆的离心率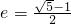，得到a，b，c的关系，化简即可求得θ的余弦值，再根据余弦求角．
解答：∵左顶点为A，右焦点为F，上顶点为B，∴A（-a，0），B（0，b），C（c，0）
∴=（-a，-b），=（c，-b）
∴cosθ=
=
又∵椭圆离心率，∴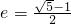
=
，
=
∴cosθ=0，θ=90°
故答案为90°
点评：本题主要借助椭圆的离心率，以及向量的数量及公式求角的大小，属于圆锥曲线，向量，以及三角函数的综合．
分析：把直线AB与FB的夹角看做向量
与向量的夹角，分别求出两个向量的坐标，代入向量的数量积公式，利用椭圆的离心率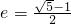，得到a，b，c的关系，化简即可求得θ的余弦值，再根据余弦求角．解答：∵左顶点为A，右焦点为F，上顶点为B，∴A（-a，0），B（0，b），C（c，0）
∴
=（-a，-b），=（c，-b）∴cosθ=
=又∵椭圆离心率
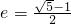，∴=，=∴cosθ=0，θ=90°
故答案为90°
点评：本题主要借助椭圆的离心率，以及向量的数量及公式求角的大小，属于圆锥曲线，向量，以及三角函数的综合．
练习册系列答案
优生乐园系列答案
相关题目
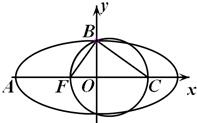如图，F是椭圆