题目内容
已知函数 (x∈R),且
(x∈R),且 .
.
(1)判断函数y=f(x)在R上的单调性,并用定义法证明;
(2)若 ,求x的取值范围.
,求x的取值范围.
解:(1)由已知得 ,m3=8,∴m=2…(3分)
,m3=8,∴m=2…(3分)
∴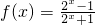 =
=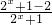 =
=
任取x1,x2∈R,且x1<x2则 =
= =
=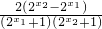
∵ ,∴
,∴
又∵x2>x1,∴ ,∴
,∴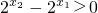
∴ ,即f(x2)-f(x1)>0,f(x2)>f(x1)
,即f(x2)-f(x1)>0,f(x2)>f(x1)
∴函数y=f(x)在R上为单调增函数. …(9分)
(2)∵ ,由(1)知函数y=f(x)在R上为单调增函数,
,由(1)知函数y=f(x)在R上为单调增函数,
∴ ,
,
化简得 ,
,
∴ …(14分)(不写集合形式不扣分)
…(14分)(不写集合形式不扣分)
分析:(1)由 求出m的值,得到函数f(x)的解析式.任取x1,x2∈R,且x1<x2,我们构造出f(x2)-f(x1)的表达式,根据实数的性质,我们易出f(x2)-f(x1)的符号,进而根据函数单调性的定义,得到答案.
求出m的值,得到函数f(x)的解析式.任取x1,x2∈R,且x1<x2,我们构造出f(x2)-f(x1)的表达式,根据实数的性质,我们易出f(x2)-f(x1)的符号,进而根据函数单调性的定义,得到答案.
(2)由(1)知函数y=f(x)在R上为单调增函数,根据题意脱去函数符号“f“,转化为关于x的分式不等式,解之即得.
点评:本题考查的知识点是函数单调性的判断与证明,其中作差法(定义法)证明函数的单调性是我们中学阶段证明函数单调性最重要的方法,一定要掌握其解的格式和步骤.
 ,m3=8,∴m=2…(3分)
,m3=8,∴m=2…(3分)∴
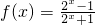 =
=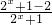 =
=
任取x1,x2∈R,且x1<x2则
 =
= =
=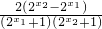
∵
 ,∴
,∴
又∵x2>x1,∴
 ,∴
,∴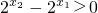
∴
 ,即f(x2)-f(x1)>0,f(x2)>f(x1)
,即f(x2)-f(x1)>0,f(x2)>f(x1)∴函数y=f(x)在R上为单调增函数. …(9分)
(2)∵
 ,由(1)知函数y=f(x)在R上为单调增函数,
,由(1)知函数y=f(x)在R上为单调增函数,∴
 ,
,化简得
 ,
,∴
 …(14分)(不写集合形式不扣分)
…(14分)(不写集合形式不扣分)分析:(1)由
 求出m的值,得到函数f(x)的解析式.任取x1,x2∈R,且x1<x2,我们构造出f(x2)-f(x1)的表达式,根据实数的性质,我们易出f(x2)-f(x1)的符号,进而根据函数单调性的定义,得到答案.
求出m的值,得到函数f(x)的解析式.任取x1,x2∈R,且x1<x2,我们构造出f(x2)-f(x1)的表达式,根据实数的性质,我们易出f(x2)-f(x1)的符号,进而根据函数单调性的定义,得到答案.(2)由(1)知函数y=f(x)在R上为单调增函数,根据题意脱去函数符号“f“,转化为关于x的分式不等式,解之即得.
点评:本题考查的知识点是函数单调性的判断与证明,其中作差法(定义法)证明函数的单调性是我们中学阶段证明函数单调性最重要的方法,一定要掌握其解的格式和步骤.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (x∈R).若
(x∈R).若 ,
, .求cos2x的值.
.求cos2x的值. ,x∈R,且
,x∈R,且
 ,
, ,
, ,求cos(α+β)的值.
,求cos(α+β)的值.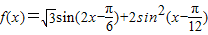 (x∈R).
(x∈R). ,x∈R
,x∈R
 ,x∈R,且
,x∈R,且
 ,
, ,
, ,求cos(α+β)的值.
,求cos(α+β)的值.