题目内容
已知:圆x2+y2=1过椭圆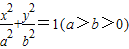 的两焦点,与椭圆有且仅有两个公共点:直线y=kx+m与圆x2+y2=1相切,与椭圆
的两焦点,与椭圆有且仅有两个公共点:直线y=kx+m与圆x2+y2=1相切,与椭圆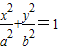 相交于A,B两点记
相交于A,B两点记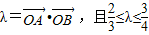 .
.(Ⅰ)求椭圆的方程;
(Ⅱ)求k的取值范围;
(Ⅲ)求△OAB的面积S的取值范围.
【答案】分析:(Ⅰ)欲求椭圆的方程,只需求出a,b的值,因为圆x2+y2=1过椭圆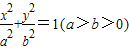 的两焦点,可求出a,因为圆x2+y2=1与椭圆有且仅有两个公共点,可求出b,椭圆的方程可知.
的两焦点,可求出a,因为圆x2+y2=1与椭圆有且仅有两个公共点,可求出b,椭圆的方程可知.
(Ⅱ)因为直线y=kx+m与圆x2+y2=1相切,可把m用k表示,再让直线方程与椭圆方程联立,把λ用k表示,根据λ的范围,就可求出k的范围.
(Ⅲ)因为△OAB的面积S= |AB|•d,把|AB|用k表示,d=1,这样,S就可用含k的式子表示了,再把(2)中求出的k的范围代入,就可得到△OAB的面积S的取值范围.
|AB|•d,把|AB|用k表示,d=1,这样,S就可用含k的式子表示了,再把(2)中求出的k的范围代入,就可得到△OAB的面积S的取值范围.
解答:解;(Ⅰ)由题意知,椭圆的焦距2c=2∴c=1
又∵圆x2+y2=1与椭圆有且仅有两个公共点,∴b=1,∴a=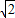
∴圆的方程为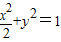
(Ⅱ)∵直线y=kx+m与圆x2+y2=1相切,∴原点O到直线的距离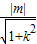 =1,即m2=k2+1
=1,即m2=k2+1
把直线y=kx+m代入椭圆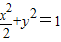 ,可得(1+2k2)x2+4kmx+2m2-2=0
,可得(1+2k2)x2+4kmx+2m2-2=0
设A(x1,y1),B(x1,y2),则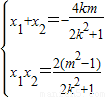
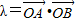 =x1x2+y1y2=(1+k2)x1x2+km(x1+x2)+m2
=x1x2+y1y2=(1+k2)x1x2+km(x1+x2)+m2
=(1+k2)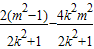 +m2
+m2
∵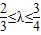 ,∴
,∴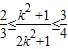 ,解得,
,解得, ≤k2≤1
≤k2≤1
∴k的取值范围是[-1,-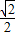 ]∪[
]∪[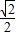 ,1];
,1];
(Ⅲ)|AB|2=(x1-x2)2+(y1-y2)2=(1+k2)(x1-x2)2
=(1+k2)[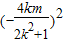 -4
-4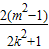 ]=(1+k2)[
]=(1+k2)[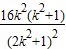 -
-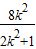 ]
]
=(1+k2)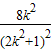 =2-
=2-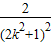
S△OAB2= |AB|2×1=
|AB|2×1= (
(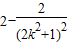 )
)
∵ ≤k2≤1,∴
≤k2≤1,∴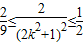
∴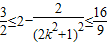 ,∴
,∴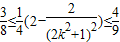
即 ≤S△OAB2=≤
≤S△OAB2=≤
∴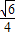 ≤S△OAB≤
≤S△OAB≤
∴△OAB的面积S的取值范围为[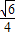 ,
, ]
]
点评:本题考查了椭圆方程的求法,以及椭圆与直线的位置关系的判断.做题时要细心.
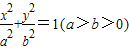 的两焦点,可求出a,因为圆x2+y2=1与椭圆有且仅有两个公共点,可求出b,椭圆的方程可知.
的两焦点,可求出a,因为圆x2+y2=1与椭圆有且仅有两个公共点,可求出b,椭圆的方程可知.(Ⅱ)因为直线y=kx+m与圆x2+y2=1相切,可把m用k表示,再让直线方程与椭圆方程联立,把λ用k表示,根据λ的范围,就可求出k的范围.
(Ⅲ)因为△OAB的面积S=
 |AB|•d,把|AB|用k表示,d=1,这样,S就可用含k的式子表示了,再把(2)中求出的k的范围代入,就可得到△OAB的面积S的取值范围.
|AB|•d,把|AB|用k表示,d=1,这样,S就可用含k的式子表示了,再把(2)中求出的k的范围代入,就可得到△OAB的面积S的取值范围.解答:解;(Ⅰ)由题意知,椭圆的焦距2c=2∴c=1
又∵圆x2+y2=1与椭圆有且仅有两个公共点,∴b=1,∴a=
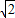
∴圆的方程为
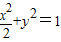
(Ⅱ)∵直线y=kx+m与圆x2+y2=1相切,∴原点O到直线的距离
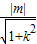 =1,即m2=k2+1
=1,即m2=k2+1把直线y=kx+m代入椭圆
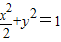 ,可得(1+2k2)x2+4kmx+2m2-2=0
,可得(1+2k2)x2+4kmx+2m2-2=0设A(x1,y1),B(x1,y2),则
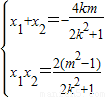
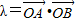 =x1x2+y1y2=(1+k2)x1x2+km(x1+x2)+m2
=x1x2+y1y2=(1+k2)x1x2+km(x1+x2)+m2=(1+k2)
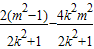 +m2
+m2∵
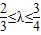 ,∴
,∴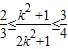 ,解得,
,解得, ≤k2≤1
≤k2≤1∴k的取值范围是[-1,-
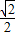 ]∪[
]∪[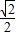 ,1];
,1];(Ⅲ)|AB|2=(x1-x2)2+(y1-y2)2=(1+k2)(x1-x2)2
=(1+k2)[
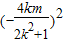 -4
-4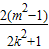 ]=(1+k2)[
]=(1+k2)[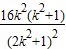 -
-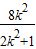 ]
]=(1+k2)
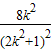 =2-
=2-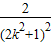
S△OAB2=
 |AB|2×1=
|AB|2×1= (
(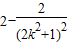 )
)∵
 ≤k2≤1,∴
≤k2≤1,∴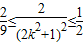
∴
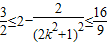 ,∴
,∴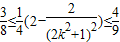
即
 ≤S△OAB2=≤
≤S△OAB2=≤
∴
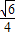 ≤S△OAB≤
≤S△OAB≤
∴△OAB的面积S的取值范围为[
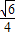 ,
, ]
]点评:本题考查了椭圆方程的求法,以及椭圆与直线的位置关系的判断.做题时要细心.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目