题目内容
 如图,AB是⊙O的纸巾,AC是弦,∠BAC的平分线交⊙O于D,DE⊥AC,交AC的延长线于E,OE交AD于F
如图,AB是⊙O的纸巾,AC是弦,∠BAC的平分线交⊙O于D,DE⊥AC,交AC的延长线于E,OE交AD于F
(1)求证:DE是⊙O的切线;
(2)若AC=4 AB=10 ,求 的值。
的值。
(I)证明:连结OD,
可得∠ODA=∠OAD=∠DAC .
∴OD//AE .
又AE⊥DE , ∴OE⊥OD,又OD为半径.
∴DE是的⊙O切线.……………5分
(II)解:过D作DH⊥AB于H,
则有∠DOH=∠CAB .
 . ……………6分
. ……………6分
 OD=5,AB=10,OH=2,
OD=5,AB=10,OH=2,
 .
.
由△AED≌△AHD可得AE=AH=7, ……………8分
又由△AEF∽△DOF 可得 ,
,
 . ………………………10分
. ………………………10分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 )
)
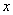 以及甲、乙成绩的方差;
以及甲、乙成绩的方差; ,
, ,则
,则 = .
= .
 B、
B、 C、
C、 D、
D、

 满足
满足 ,其中
,其中 ,设
,设 ,则
,则 等于( )
等于( ) B.
B. C.
C. D.
D.
 ,则a-b=________.
,则a-b=________.  的值为
的值为 