题目内容
20．已知向量$\vec a=（1，2）$，向量$\vec b=（-3，2）$．（Ⅰ）若向量$\overrightarrow a+k\vec b$与向量$\overrightarrow a-3\vec b$垂直，求实数k的值；
（Ⅱ）当k为何值时，向量$\overrightarrow a+k\vec b$与向量$\overrightarrow a-3\vec b$平行？并说明它们是同向还是反向．
分析 由已知向量的坐标求出$\overrightarrow a+k\vec b$与$\overrightarrow a-3\vec b$的坐标．
（Ⅰ）直接由向量垂直的坐标表示列式求实数k的值；
（Ⅱ）由向量共线的坐标运算求得k值，代入向量验证是同向还是反向．
解答 解：∵$\vec a=（1，2）$，$\vec b=（-3，2）$，
∴$\overrightarrow a+k\vec b$=（1-3k，2+2k），$\overrightarrow a-3\vec b$=（10，-4），
（Ⅰ）若向量$\overrightarrow a+k\vec b$与向量$\overrightarrow a-3\vec b$垂直，则10（1-3k）-4（2+2k）=0，解得：k=$\frac{1}{19}$；
（Ⅱ）若向量$\overrightarrow a+k\vec b$与向量$\overrightarrow a-3\vec b$平行，则-4（1-3k）-10（2+2k）=0，解得：k=-3．
此时$\overrightarrow a+k\vec b$=（10，-4），$\overrightarrow a-3\vec b$=（10，-4），两向量同向．
点评 本题考查平面向量的数量积运算，考查了向量平行和垂直的坐标运算，是中档题．
练习册系列答案
习题精选系列答案
相关题目
11．已知一个平面α，那么对于空间内的任意一条直线l，在平面α内一定存在一条直线m，使得直线l与直线m（ ）
| A． | 平行 | B． | 相交 | C． | 异面 | D． | 垂直 |
8．设集合A={2，5}，集合B={1，2}，集合C={1，2，5，7}，则（A∪B）∩C为（ ）
| A． | {1，2，5} | B． | {2，5} | C． | {2，5，7} | D． | {1，2，5，7} |
15．已知集合M={1，2，3}，N={2，3，4，5}，那么M∩N=（ ）
| A． | ∅ | B． | {1，4，5} | C． | {1，2，3，4，5} | D． | {2，3} |
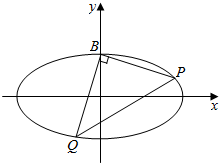如图，已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的离心率是$\frac{{\sqrt{3}}}{2}$，一个顶点是B（0，1）．