题目内容
(本小题满分11分)(注意:在试题卷上作答无效)
已知 为坐标原点,向量
为坐标原点,向量 ,点
,点 是直线
是直线 上的一点,且点
上的一点,且点 分有向线段
分有向线段 的比为
的比为 .
.
(1)记函数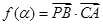 ,
, ,讨论函数
,讨论函数 的单调性,并求其值域;
的单调性,并求其值域;
(2)若 三点共线,求
三点共线,求 的值.
的值.
已知
 为坐标原点,向量
为坐标原点,向量 ,点
,点 是直线
是直线 上的一点,且点
上的一点,且点 分有向线段
分有向线段 的比为
的比为 .
.(1)记函数
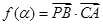 ,
, ,讨论函数
,讨论函数 的单调性,并求其值域;
的单调性,并求其值域;(2)若
 三点共线,求
三点共线,求 的值.
的值.(1)函数 的单调递增区间为
的单调递增区间为 ,单调递减区间为
,单调递减区间为 ,
,
 ,其值域为
,其值域为 ;
;
(2)
 。
。
 的单调递增区间为
的单调递增区间为 ,单调递减区间为
,单调递减区间为 ,
,  ,其值域为
,其值域为 ;
;(2)

 。
。(1)设P(x,y),根据点B分有向线段 的比为1,可知点B为线段AP的中点,根据中点坐标公式可求出P的坐标.进而可求出
的比为1,可知点B为线段AP的中点,根据中点坐标公式可求出P的坐标.进而可求出 关于
关于 的函数关系式,再求值域.
的函数关系式,再求值域.
(2)根据O、P、C三点共线所以 ,根据向量平行的坐标表示,可求出
,根据向量平行的坐标表示,可求出 的值.
的值.
由于 ,由
,由 求出
求出 代入左边式子即可.
代入左边式子即可.
依题意知: ,设点
,设点 的坐标为
的坐标为 ,则:
,则:
 ,所以
,所以 ,点
,点 的坐标为
的坐标为

 ......2分
......2分
(1)



 ,......4分
,......4分
由 可知函数
可知函数 的单调递增区间为
的单调递增区间为 ,
,
单调递减区间为 ,......6分
,......6分
所以 ,其值域为
,其值域为 ;......8分
;......8分
(2)由 三点共线的
三点共线的 ,......10分
,......10分

 ,
,

 .......12分
.......12分
 的比为1,可知点B为线段AP的中点,根据中点坐标公式可求出P的坐标.进而可求出
的比为1,可知点B为线段AP的中点,根据中点坐标公式可求出P的坐标.进而可求出 关于
关于 的函数关系式,再求值域.
的函数关系式,再求值域.(2)根据O、P、C三点共线所以
 ,根据向量平行的坐标表示,可求出
,根据向量平行的坐标表示,可求出 的值.
的值.由于
 ,由
,由 求出
求出 代入左边式子即可.
代入左边式子即可.依题意知:
 ,设点
,设点 的坐标为
的坐标为 ,则:
,则: ,所以
,所以 ,点
,点 的坐标为
的坐标为
 ......2分
......2分(1)




 ,......4分
,......4分由
 可知函数
可知函数 的单调递增区间为
的单调递增区间为 ,
,单调递减区间为
 ,......6分
,......6分 所以
 ,其值域为
,其值域为 ;......8分
;......8分(2)由
 三点共线的
三点共线的 ,......10分
,......10分
 ,
,

 .......12分
.......12分
练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
 )的一段图象如图所示.
)的一段图象如图所示.
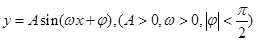 相邻的两个最高点和最低点分别为
相邻的两个最高点和最低点分别为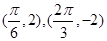
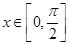 时,该函数的值域
时,该函数的值域 在区间
在区间 上的值域为_______________.
上的值域为_______________. .
. 的最小正周期;
的最小正周期; 的图象是由
的图象是由 的图象向右平移
的图象向右平移 个单位长度,再向上平移1个单位长度得到的,当
个单位长度,再向上平移1个单位长度得到的,当 [
[ ,
, ]时,求
]时,求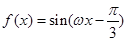
 和
和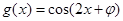 的图象的对称中心完全相同,若
的图象的对称中心完全相同,若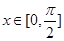 ,则
,则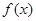 的最小值是
的最小值是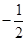 B.
B.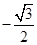 C.
C.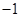 D.
D.
 (A>0,
(A>0, >0)的部分图像如图所示,则
>0)的部分图像如图所示,则 ……
…… 的值为( )
的值为( ) 


 的图象过
的图象过 ,且
,且 内角A、B、C所对应边分别为a、b、c,若
内角A、B、C所对应边分别为a、b、c,若
 的值及
的值及 的单调递增区间
的单调递增区间 ,
, ,
, ,
,
 的值;(2)求
的值;(2)求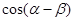 的值。
的值。