题目内容
已知函数
(Ⅰ)求函数f(x)的最小正周期和最小值;
(Ⅱ)设△ABC的内角A,B,C对边分别为 与
与 垂直,求a,b的值.
垂直,求a,b的值.
解:(Ⅰ)∵ (2分)
(2分)
令 ,∴函数f(x)的单调递增区间为
,∴函数f(x)的单调递增区间为 ,
,
 (4分)
(4分)
(Ⅱ)由题意可知, ,∴
,∴ ,∵0<C<π,∴
,∵0<C<π,∴ (舍)或
(舍)或 (6分)∵
(6分)∵ 垂直,∴2sinA-sinB=0,即2a=b(8分)∵
垂直,∴2sinA-sinB=0,即2a=b(8分)∵ ②(10分)
②(10分)
由①②解得,a=1,b=2.(12分)
分析:(I)利用二倍角公式即公式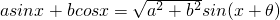 化简f(x);利用三角函数的周期公式求出周期;令整体角在正弦的递增区间上求出x的范围即为递增区间.
化简f(x);利用三角函数的周期公式求出周期;令整体角在正弦的递增区间上求出x的范围即为递增区间.
(II)先求出角C,利用向量垂直的充要条件列出方程得到边a,b的关系;利用余弦定理得到a,b,c的关系,求出a,b.
点评:本题考查三角函数的二倍角公式、考查三角函数的公式 、考查求三角函数的性质常用的方法是整体角处理的方法、考查三角形中的余弦定理.
、考查求三角函数的性质常用的方法是整体角处理的方法、考查三角形中的余弦定理.
 (2分)
(2分)令
 ,∴函数f(x)的单调递增区间为
,∴函数f(x)的单调递增区间为 ,
, (4分)
(4分)(Ⅱ)由题意可知,
 ,∴
,∴ ,∵0<C<π,∴
,∵0<C<π,∴ (舍)或
(舍)或 (6分)∵
(6分)∵ 垂直,∴2sinA-sinB=0,即2a=b(8分)∵
垂直,∴2sinA-sinB=0,即2a=b(8分)∵ ②(10分)
②(10分)由①②解得,a=1,b=2.(12分)
分析:(I)利用二倍角公式即公式
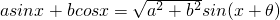 化简f(x);利用三角函数的周期公式求出周期;令整体角在正弦的递增区间上求出x的范围即为递增区间.
化简f(x);利用三角函数的周期公式求出周期;令整体角在正弦的递增区间上求出x的范围即为递增区间.(II)先求出角C,利用向量垂直的充要条件列出方程得到边a,b的关系;利用余弦定理得到a,b,c的关系,求出a,b.
点评:本题考查三角函数的二倍角公式、考查三角函数的公式
 、考查求三角函数的性质常用的方法是整体角处理的方法、考查三角形中的余弦定理.
、考查求三角函数的性质常用的方法是整体角处理的方法、考查三角形中的余弦定理. 
练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目

