Question

（文）已知函数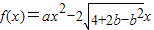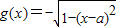，，（a，b∈R）
（Ⅰ）当b=0时，若f（x）在[2，+∞）上单调递增，求a的取值范围；
（Ⅱ）求满足下列条件的所有实数对（a，b）：当a是整数时，存在x，使得f（x）是f（x）的最大值，g（x）是g（x）的最小值；
（Ⅲ）对满足（Ⅱ）的条件的一个实数对（a，b），试构造一个定义在D={x|x＞-2，且x≠2k-2，k∈N}上的函数h（x），使当x∈（-2，0）时，h（x）=f（x），当x∈D时，h（x）取得最大值的自变量的值构成以x为首项的等差数列．

Answer 1

【答案】分析：（Ⅰ）当b=0，时，f（x）=ax²-4x，讨论a的取值，结合二次函数的单调性建立a的不等关系即可；
（Ⅱ）讨论a为0时不可能，要使f（x）有最大值，必须满足 ，求出此时的x=x，根据g（x）取最小值时，x=x=a，建立等量关系，结合a是整数，求出a和b的值．
（Ⅲ）当实数对（a，b）是（-1，-1），（-1，3）时，f（x）=-x²-2x，依题意，只需构造以2（或2的正整数倍）为周期的周期函数即可．
解答：解：（Ⅰ）当b=0时，f（x）=ax²-4x，
若a=0，f（x）=-4x，则f（x）在[2，+∞）上单调递减，不符题意．
故a≠0，要使f（x）在[2，+∞）上单调递增，必须满足，∴a≥1．
（Ⅱ）若a=0，，则f（x）无最大值，故a≠0，∴f（x）为二次函数，
要使f（x）有最大值，必须满足，即a＜0且，
此时，时，f（x）有最大值．
又g（x）取最小值时，x=x=a，依题意，有，则，
∵a＜0且，∴，得a=-1，此时b=-1或b=3．
∴满足条件的实数对（a，b）是（-1，-1），（-1，3）．
（Ⅲ）当实数对（a，b）是（-1，-1），（-1，3）时，f（x）=-x²-2x
依题意，只需构造以2（或2的正整数倍）为周期的周期函数即可．
如对x∈（2k-2，2k），k∈N，x-2k∈（-2，0），
此时，h（x）=h（x-2k）=f（x-2k）=-（x-2k）²-2（x-2k），
故h（x）=-（x-2k）²-2（x-2k），x∈（2k-2，2k），k∈N．
点评：本题考查的是数列与不等式的综合问题．等差关系的确定、函数单调性的应用，以及函数的最值及其几何意义，属于中档题．