题目内容
四棱锥P—ABCD的底面是边长为1的正方形,PD⊥平面ABCD,若侧面PAB与侧面PCD所成的角为45°.(Ⅰ)求点C到平面PAB的距离;
(Ⅱ)侧棱PB上是否存在一点E,使PB⊥平面ACE.若存在,确定点E的位置;若不存在,说明理由.
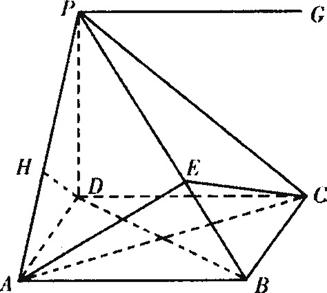
解:(1)设PG=平面ABP∩平面PCD,

∵AB∥CD ∴CD∥平面PAB,
又∵CD![]() 平面PCD,∴CD∥PG,
平面PCD,∴CD∥PG,
∵PD⊥平面ABCD,∴PD⊥CD,又CD⊥AD,
∴CD⊥平面PAD,PG⊥平面PAD,∴PG⊥PA,PG⊥PD,
∴∠APD为侧面PAB与侧面PCD所成二面角的平面角,
∴∠APD=45°, 又AD=1,PD⊥AD,∴PD=1.
∵CD∥平面PAB,
∴点D到平面PAB的距离等于点C到平面PAB的距离.作DH⊥PA于H,可证DH为点D到平面PAB的距离,DH=![]() ,
,
∴点C到平面PAB的距离为![]() .
.
(Ⅱ)存在点E使PB⊥平面AEC.
连结BD,BD⊥平面AC,又BD⊥AC,∴PB⊥AC
若PB⊥平面ACE,只需PB⊥AE,
PA=![]() ,AB=1,PB=
,AB=1,PB=![]() ,AE=
,AE=![]() ,PE=
,PE=![]() ,
,
∴当![]() 时,PB⊥平面AEC.
时,PB⊥平面AEC.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
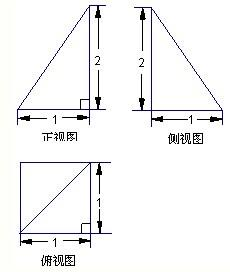 已知四棱锥P-ABCD的三视图如图所示,则这个四棱锥的体积为( )
已知四棱锥P-ABCD的三视图如图所示,则这个四棱锥的体积为( )A、
| ||
| B、1 | ||
C、
| ||
D、
|
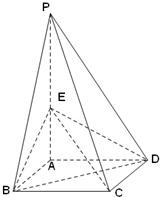 如图,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是PA的中点.
如图,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是PA的中点. 如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,侧面PBC内有BE⊥PC于E,且BE=
如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,侧面PBC内有BE⊥PC于E,且BE= 如图,ABCD是正方形,O是该正方形的中心,P是平面ABCD外一点,PO⊥底面ABCD,E是PC的中点.求证:
如图,ABCD是正方形,O是该正方形的中心,P是平面ABCD外一点,PO⊥底面ABCD,E是PC的中点.求证: