题目内容
17.随着网络营销和电子商务的兴起,人们的购物方式更具多样化,某调查机构随机抽取10名购物者进行采访,5名男性购物者中有3名倾向于选择网购,2名倾向于选择实体店;5名女性购物者中有2名倾向于选择网购,3名倾向于选择实体店.(Ⅰ)若从这10名购物者中随机抽取4名,求至多有一名倾向于选择实体店的女性购物者的概率;
(Ⅱ)若分别从男性购物者和女性购物者中各随机抽取2名,设X表示抽到倾向于选择网购的人数,求X的分布列和数学期望.
分析 (Ⅰ)设“至多有1名倾向于选择实体店的女性购物者”为事件A,利用互斥事件的概率公式计算即可;
(Ⅱ)根据题意知X的取值,计算对应的概率值,写出随机变量X的分布列,计算数学期望值.
解答 解:(Ⅰ)设“至多有1名倾向于选择实体店的女性购物者”为事件A,
则P(A)=$\frac{{C}_{3}^{1}{•C}_{7}^{3}}{{C}_{10}^{4}}$+$\frac{{C}_{3}^{0}{•C}_{7}^{4}}{{C}_{10}^{4}}$=$\frac{2}{3}$;
(Ⅱ)根据题意,X的取值为0,1,2,3,4;
则P(X=0)=$\frac{{C}_{2}^{2}{•C}_{3}^{2}}{{C}_{5}^{2}{•C}_{5}^{2}}$=$\frac{3}{100}$,
P(X=1)=$\frac{{C}_{3}^{1}{•C}_{2}^{1}{•C}_{3}^{2}{+C}_{2}^{2}{•C}_{2}^{1}{•C}_{3}^{1}}{{C}_{5}^{2}{•C}_{5}^{2}}$=$\frac{24}{100}$,
P(X=2)=$\frac{{C}_{3}^{1}{•C}_{2}^{1}{•C}_{2}^{1}{•C}_{3}^{1}{+C}_{3}^{2}{•C}_{3}^{2}{+C}_{2}^{2}{•C}_{2}^{2}}{{C}_{5}^{2}{•C}_{5}^{2}}$=$\frac{46}{100}$,
P(X=3)=$\frac{{C}_{3}^{2}{•C}_{2}^{1}{•C}_{3}^{1}{+C}_{3}^{1}{•C}_{2}^{1}{•C}_{2}^{2}}{{C}_{5}^{2}{•C}_{5}^{2}}$=$\frac{24}{100}$,
P(X=4)=$\frac{{C}_{3}^{2}{•C}_{2}^{2}}{{C}_{5}^{2}{•C}_{5}^{2}}$=$\frac{3}{100}$;
∴随机变量X的分布列为:
| X | 0 | 1 | 2 | 3 | 4 |
| P | $\frac{3}{100}$ | $\frac{24}{100}$ | $\frac{46}{100}$ | $\frac{24}{100}$ | $\frac{3}{100}$ |
点评 本题考查了古典概型的概率计算问题,也考查了离散型随机变量的分布列与数学期望的计算问题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | $\frac{4}{5}$ | B. | $\frac{6}{5}$ | C. | $\frac{8}{5}$ | D. | 2 |
| A. | (-∞$\frac{1}{3}$]∪[3,+∞) | B. | [$\frac{1}{3}$,3] | C. | [$\frac{1}{3}$,1] | D. | [1,3] |
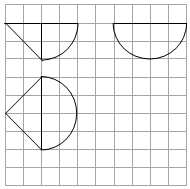 某组合体的三视图如图所示,图中网格每个小正方形的边长为1,曲线均为圆弧的一部分,则该几何体的体积为( )
某组合体的三视图如图所示,图中网格每个小正方形的边长为1,曲线均为圆弧的一部分,则该几何体的体积为( )| A. | $\frac{28}{3}π$ | B. | 4π | C. | $\frac{10}{3}π$ | D. | $\frac{2}{3}+\frac{8}{3}π$ |
| x | 0 | 1 | 3 | 4 |
| y | 22 | 35 | 48 | 75 |
| A. | 22 | B. | 26 | C. | 33.6 | D. | 19.5 |
 如图,长方体ABCD-A1B1C1D1中,点M在棱BB1上,两条直线MA,MC与平面ABCD所成角均为θ,AC与BD交于点O.
如图,长方体ABCD-A1B1C1D1中,点M在棱BB1上,两条直线MA,MC与平面ABCD所成角均为θ,AC与BD交于点O.