题目内容
13.若函数t=f(x)的值域为(0,8],则y=t2-10t-4的值域为( )| A. | [-20,-4) | B. | [-20,-4] | C. | [-29,-20] | D. | [-29,-4) |
分析 由函数t=f(x)值域为(0,8]可知f(x)∈(0,8],用配方法求函数的值域.
解答 解:F(x)=t2-10t-4=(t-5)2-29,
∵函数t=f(x)值域为(0,8],
∴0≤(t-5)2<25,
∴-29≤(t-5)2-29<-4,
故选:D.
点评 本题考查了函数值域的求法.高中函数值域求法有:1、观察法,2、配方法,3、反函数法,4、判别式法;5、换元法,6、数形结合法,7、不等式法,8、分离常数法,9、单调性法,10、利用导数求函数的值域,11、最值法,12、构造法,13、比例法.要根据题意选择.

练习册系列答案
相关题目
18.已知双曲线C:$\frac{{y}^{2}}{{a}^{2}}-\frac{{x}^{2}}{{b}^{2}}$=1(a>0,b>0)的离心率e=$\frac{\sqrt{5}}{2}$,点P是抛物线y2=4x上的一个动点,P到双曲线C的上焦点F1(0,c)的距离与到直线x=-1的距离之和的最小值为$\sqrt{6}$,则该双曲线的方程为( )
| A. | $\frac{{y}^{2}}{2}-\frac{{x}^{2}}{3}$=1 | B. | y2-$\frac{{x}^{2}}{4}$=1 | C. | $\frac{{y}^{2}}{4}$-x2=1 | D. | $\frac{{y}^{2}}{3}-\frac{{x}^{2}}{2}$=1 |
8.如图是正方体的侧面展开图,l1、l2是两条侧面对角线,则在此正方体中,l1与l2( )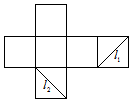

| A. | 互相平行 | B. | 相交且夹角为$\frac{π}{3}$ | C. | 异面且互相垂直 | D. | 异面且夹角为$\frac{π}{3}$ |
5.已知f(x)=4x5+3x4+2x3-x2-x-$\frac{1}{2}$,用秦九韶算法求f(-2)等于( )
| A. | -$\frac{197}{2}$ | B. | $\frac{197}{2}$ | C. | $\frac{183}{2}$ | D. | -$\frac{183}{2}$ |